题目内容
已知点A(a,b) 满足方程x-y-3=0,则由点A向圆C:x2+y2+2x-4y+3=0所作的切线长的最小值是( )
分析:将圆C化为标准方程,得出圆心为C(-1,2)、半径r=
.根据题意知点A是直线x-y-3=0上的动点,由圆的切线的性质可得当A、C的距离最小时,可使切线长最小.由此利用点到直线的距离公式与勾股定理加以计算,可得经过点A作圆C的切线所得切线长的最小值.
| 2 |
解答:解:将圆C:x2+y2+2x-4y+3=0化成标准方程,得(x+1)2+(y-2)2=2,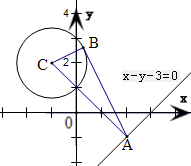
∴圆C的圆心为C(-1,2)、半径r=
.
∵点A(a,b) 满足方程x-y-3=0,
∴点A是直线x-y-3=0上的动点.
由点A向圆C作切线,设切点为B,则CB⊥AB,
根据勾股定理,可得切线长|AB|=
=
,
由此可得当|CA|达到最小时,相应地|AB|有最小值.
∵点C到直线x-y-3=0的距离为d=
=3
,
∴|CA|的最小值为3
,可得|AB|的最小值为
=4.
即经过点A作圆C的切线,切线长的最小值为4.
故答案为:C

∴圆C的圆心为C(-1,2)、半径r=
| 2 |
∵点A(a,b) 满足方程x-y-3=0,
∴点A是直线x-y-3=0上的动点.
由点A向圆C作切线,设切点为B,则CB⊥AB,
根据勾股定理,可得切线长|AB|=
| |CA|2-|CB|2 |
| |CA|2-2 |
由此可得当|CA|达到最小时,相应地|AB|有最小值.
∵点C到直线x-y-3=0的距离为d=
| |-1-2-3| | ||
|
| 2 |
∴|CA|的最小值为3
| 2 |
(3
|
即经过点A作圆C的切线,切线长的最小值为4.
故答案为:C
点评:本题着重考查了点到直线的距离公式、直线与圆的位置关系等知识,属于中档题.考查了学生灵活运用点到直线的距离公式化简求值,解题的关键是找出切线长最短时的条件,根据题意画出相应的图形.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
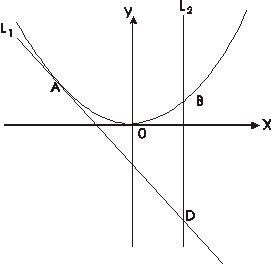 已知点A(-1,2)是抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a≠-1)交抛物线C于点B,交直线l1于点D.
已知点A(-1,2)是抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a≠-1)交抛物线C于点B,交直线l1于点D.