题目内容
已知函数y=x+ (x>0)有如下性质:如果常数a>0,那么该函数在(0,
(x>0)有如下性质:如果常数a>0,那么该函数在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数.
,+∞)上是增函数.
(1)如果函数y=x+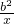 (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值;
(2)研究函数y=x2+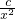 (x>0,常数c>0)在定义域内的单调性,并用定义证明(若有多个单调区间,请选择一个证明);
(x>0,常数c>0)在定义域内的单调性,并用定义证明(若有多个单调区间,请选择一个证明);
(3)对函数y=x+ 和y=x2+
和y=x2+ (x>0,常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=
(x>0,常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=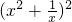 +
+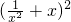 在区间[
在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
解:(1)函数y=x+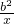 (x>0)在(0,
(x>0)在(0,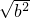 ]上是减函数,在[
]上是减函数,在[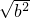 ,+∞)上是增函数.当
,+∞)上是增函数.当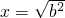 时,
时,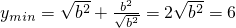 ,
,
所以b=±3.(漏-3,扣1分)…(4分)
(2)函数y=x2+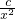 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数.…(2分)
,+∞)上是增函数.…(2分)
证明:函数y=x2+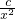 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数
]上是减函数
在(0, ]内任取两个变量x1,x2,且x1<x2,
]内任取两个变量x1,x2,且x1<x2,
则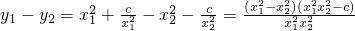
∵x1,x2∈(0, ]且x1<x2,
]且x1<x2,
∴y1>y2
∴函数y=x2+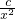 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数…(4分)
]上是减函数…(4分)
(3)作出推广:y=xn+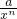 (x>0,n∈N*,常数a>0)…(1分)
(x>0,n∈N*,常数a>0)…(1分)
在(0,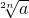 ]上是减函数,在[
]上是减函数,在[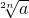 ,+∞)上是增函数.…(2分)
,+∞)上是增函数.…(2分)
或作出推广:y= +
+ (x>0,n∈N,常数a>0)…(1分)
(x>0,n∈N,常数a>0)…(1分)
在(0,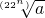 ]上是减函数,在[
]上是减函数,在[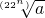 ,+∞)上是增函数.…(2分)
,+∞)上是增函数.…(2分)
F(x)=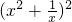 +
+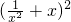
=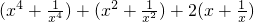
 上是减函数,在[1,2]上是增函数.…(2分)
上是减函数,在[1,2]上是增函数.…(2分)
当x=1时,F(x)min=8;
当x= 或2时,
或2时,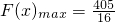 .…(3分)
.…(3分)
分析:(1)根据题意可知:函数y=x+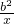 (x>0)在(0,
(x>0)在(0,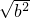 ]上是减函数,在[
]上是减函数,在[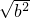 ,+∞)上是增函数.从而当
,+∞)上是增函数.从而当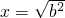 时,函数取到最小值6,故可解;
时,函数取到最小值6,故可解;
(2)根据题意可知:函数y=x2+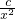 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数,再用定义进行证明;
,+∞)上是增函数,再用定义进行证明;
(3)根据题意,结合基本不等式可作推广.利用推广结论,可知函数在 上是减函数,在[1,2]上是增函数,从而可解.
上是减函数,在[1,2]上是增函数,从而可解.
点评:本题的考点是函数与方程的综合运用,主要考查与基本不等式结合,研究函数的单调性,并做推广,从而研究函数的最值.
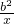 (x>0)在(0,
(x>0)在(0,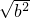 ]上是减函数,在[
]上是减函数,在[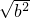 ,+∞)上是增函数.当
,+∞)上是增函数.当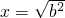 时,
时,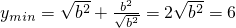 ,
,所以b=±3.(漏-3,扣1分)…(4分)
(2)函数y=x2+
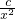 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数.…(2分)
,+∞)上是增函数.…(2分)证明:函数y=x2+
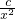 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数
]上是减函数在(0,
 ]内任取两个变量x1,x2,且x1<x2,
]内任取两个变量x1,x2,且x1<x2,则
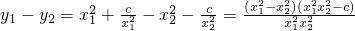
∵x1,x2∈(0,
 ]且x1<x2,
]且x1<x2,∴y1>y2
∴函数y=x2+
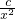 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数…(4分)
]上是减函数…(4分)(3)作出推广:y=xn+
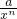 (x>0,n∈N*,常数a>0)…(1分)
(x>0,n∈N*,常数a>0)…(1分)在(0,
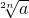 ]上是减函数,在[
]上是减函数,在[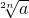 ,+∞)上是增函数.…(2分)
,+∞)上是增函数.…(2分)或作出推广:y=
 +
+ (x>0,n∈N,常数a>0)…(1分)
(x>0,n∈N,常数a>0)…(1分)在(0,
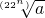 ]上是减函数,在[
]上是减函数,在[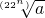 ,+∞)上是增函数.…(2分)
,+∞)上是增函数.…(2分)F(x)=
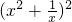 +
+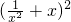
=
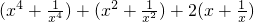
 上是减函数,在[1,2]上是增函数.…(2分)
上是减函数,在[1,2]上是增函数.…(2分)当x=1时,F(x)min=8;
当x=
 或2时,
或2时,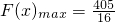 .…(3分)
.…(3分)分析:(1)根据题意可知:函数y=x+
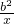 (x>0)在(0,
(x>0)在(0,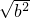 ]上是减函数,在[
]上是减函数,在[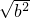 ,+∞)上是增函数.从而当
,+∞)上是增函数.从而当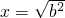 时,函数取到最小值6,故可解;
时,函数取到最小值6,故可解;(2)根据题意可知:函数y=x2+
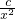 (x>0,常数c>0)在(0,
(x>0,常数c>0)在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数,再用定义进行证明;
,+∞)上是增函数,再用定义进行证明;(3)根据题意,结合基本不等式可作推广.利用推广结论,可知函数在
 上是减函数,在[1,2]上是增函数,从而可解.
上是减函数,在[1,2]上是增函数,从而可解.点评:本题的考点是函数与方程的综合运用,主要考查与基本不等式结合,研究函数的单调性,并做推广,从而研究函数的最值.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
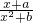 是定义在R上的奇函数,其值域为[-
是定义在R上的奇函数,其值域为[-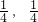 ].
]. 是定义在R上的奇函数,其值域为[-
是定义在R上的奇函数,其值域为[- ].
].