题目内容
等比数列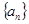 各项为正,
各项为正,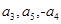 成等差数列.
成等差数列.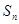 为
为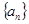 的前n项和,则
的前n项和,则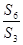 =( )
=( )
A.2 B.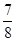 C.
C.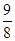 D.
D.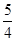
【答案】
C
【解析】
试题分析:设{an}的公比为q(q≠0,q≠1),利用 成等差数列结合通项公式,可得
成等差数列结合通项公式,可得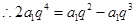 ,由此即可求得数列{an}的公比,进而求出数列的前n项和公式,可得答案
,由此即可求得数列{an}的公比,进而求出数列的前n项和公式,可得答案
设{an}的公比为q(q>0,q≠1)
∵ 成等差数列,∴
成等差数列,∴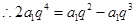
∵a1≠0,q≠0,∴2q2+q-1=0,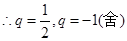 ,故
,故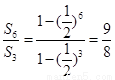 ,故选C.
,故选C.
考点:等比数列的公式运用
点评:解决该试题的关键是对于数列公式的熟练表示和运用,属于基础题 。

练习册系列答案
相关题目
等比数列![]() 各项为正,
各项为正,![]() 成等差数列,
成等差数列,![]() 为
为![]() 的前
的前![]() 项和,则
项和,则![]() ( )
( )
| A. | B. | C. | D. |