题目内容

设函数

(1)解不等式；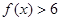

(2)若关于的不等式的解集不是空集，求得取值范围．

 

【答案】

（1）；（2）或.

【解析】

试题分析：本题考查绝对值不等式的解法和有解问题的求法，考查学生运用函数零点分类讨论的解题思想和转化思想.第一问，利用函数零点分成3类不等式组；第二问，是有解问题，将问题转化为，本问的关键是求，将函数去掉绝对值，化成分段函数，通过数形结合求出，即，下面解绝对值不等式求出的取值范围.

试题解析：（1）∵  ，

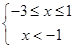∴ 或 或，

∴或 或 ，

∴或或 ，

∴或.            5分

（2）因为，

所以，

所以若的解集不是空集，则，

解得：或，

即的取值范围是：或.         10分

考点：1.绝对值不等式的解法；2.分段函数的最值；3.有解问题的解法.

 

练习册系列答案
相关题目
给出以下四个命题：
①设a是实数，i是虚数单位，若
a
1+i
+
1+i
2
是实数，则a=1；
②不等|x-1|+|x-2|≤2的解集为[
1
2
，
5
2
]；
③
∫
e
1
(ex-
2
x
)dx=ee-e-2；
④已知命题p：在△ABC中，如果cos2A=cos2B，则A=B；命题q：y=
1
x
在定义城内是减函数，则“p∧q”为真，“p∧q”为假，“￢p”为真．
其中正确命题的序号是
 
．（请把正确的序号全部填上）
（2011•武昌区模拟）设函数f（x）=2x3-3（a+3）x2+18ax-8a，x∈R．
（Ⅰ）当a=-1时，求函数f（x）的极值；
（Ⅱ）若函数f（x）在区间[1，2]上为减函数，求实数a的取值范围；
（Ⅲ）当方程f（x）=0有三个不等的正实数解时，求实数a的取值范围．


（本小题满分10分）选修4-5不等选讲
设函数（1）当时，求不等式的解集；(2)如果不等式的解集为，求的值。
设函数f（x）=2x3-3（a+3）x2+18ax-8a，x∈R。
（1）当a=-1时，求函数f（x）的极值；
（2）若函数f（x）在区间[1，2]上为减函数，求实数a的取值范围；
（3）当方程f（x）=0有三个不等的正实数解时，求实数a的取值范围。
给出以下四个命题：
①设a是实数，i是虚数单位，若是实数，则a=1；
②不等|x-1|+|x-2|≤2的解集为；
③；
④已知命题p：在△ABC中，如果cos2A=cos2B，则A=B；命题在定义城内是减函数，则“p∧q”为真，“p∧q”为假，“￢p”为真．
其中正确命题的序号是    ．（请把正确的序号全部填上）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网