题目内容
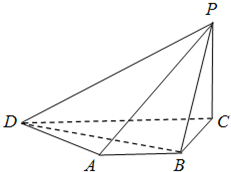（2009•西城区一模）如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，∠BCD=90°，AB∥CD，又AB=BC=PC=1， PB=| 2 |
（Ⅰ）求证：PC⊥平面ABCD；
（Ⅱ）求二面角B-PD-C的大小；
（Ⅲ）求点B到平面PAD的距离．
分析：（1）要证PC⊥平面ABCD可利用线面垂直的判定定理即证明PC与面ABCD内的两条相交直线垂直即可而根据题中的条件分析可知AB，BC即为要找的两条相交直线．
（Ⅱ）法一：几何法．可先利用题中条件作出过其中一平面内的一点垂直于另一平面的垂线然后再根据三垂线定理即可作出二面角的平面角然后把这个角放在三角形内求解即可．而根据题中的条件再结合（1）的结论可得BC⊥平面PCD故过C作CM⊥PD于M连接BM而CM是BM在平面PCD内的射影根据三垂线定理可得BM⊥PD所以∠CMB为二面角B-PD-C的平面角然后在直角三角形BCM中求出∠CMB．
法二：空间向量法．根据题中条件可得CD，CB，CA两两垂直故可建立如图所示的空间直角坐标系过C作CM⊥DP于M，连接BM利用
⊥
，
，
共线可求出M点的坐标为(
， 0，
)从而可计算出
•
=
+0-
=0即MB⊥DP故∠CMB为二面角B-PD-C的平面角然后利用向量的夹角公式即可求出∠CMB的余弦值．
（Ⅲ）设点B到平面PAD的距离为h利用三棱锥B-PAD与三棱锥P-ABD的体积相等即可求出h．
（Ⅱ）法一：几何法．可先利用题中条件作出过其中一平面内的一点垂直于另一平面的垂线然后再根据三垂线定理即可作出二面角的平面角然后把这个角放在三角形内求解即可．而根据题中的条件再结合（1）的结论可得BC⊥平面PCD故过C作CM⊥PD于M连接BM而CM是BM在平面PCD内的射影根据三垂线定理可得BM⊥PD所以∠CMB为二面角B-PD-C的平面角然后在直角三角形BCM中求出∠CMB．
法二：空间向量法．根据题中条件可得CD，CB，CA两两垂直故可建立如图所示的空间直角坐标系过C作CM⊥DP于M，连接BM利用
| MC |
| DP |
| DM |
| DP |
| 2 |
| 5 |
| 4 |
| 5 |
| MB |
| DP |
| 4 |
| 5 |
| 4 |
| 5 |
（Ⅲ）设点B到平面PAD的距离为h利用三棱锥B-PAD与三棱锥P-ABD的体积相等即可求出h．
解答：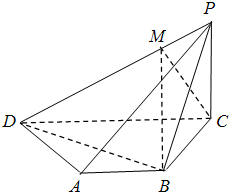
解：（Ⅰ）证明：∵在△PBC中，BC=PC=1， PB=
∴BC2+PC2=PB2
∴∠PCB=90°，即PC⊥BC
∵AB⊥PC
∵AB∩BC=B
∴PC⊥平面ABCD．
（Ⅱ）方法一：由（Ⅰ）知PC⊥BC
又∵BC⊥CD，PC∩CD=C
∴BC⊥平面PCD
过C作CM⊥PD于M，连接BM
∴CM是BM在平面PCD内的射影
∴BM⊥PD，
又∵CM⊥PD
∴∠CMB为二面角B-PD-C的平面角．
在△PCD中，∠PCD=90°，PC=1，CD=2，∴PD=
=
又∵CM⊥PD∴PD•CM=PC•CD，∴CM=
=
．
在△CMB中，∠BCM=90°，BC=1，CM=
∴tan∠CMB=
=
∴二面角B-PD-C的大小为arctan
．
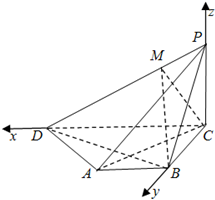
方法二：如图，在平面ABCD内，以C为原点，CD、CB、CP分别为x、y、z轴，建立空间直角坐标系C-xyz，
则C（0，0，0），B（0，1，0），D（2，0，0），P（0，0，1），A（1，1，0）
过C作CM⊥DP于M，连接BM，设M（x，y，z）
则
=(-x，-y，-z)，
=(x-2，y，z)，
=(-2，0，1)
∵
⊥
∴
•
=2x-z=0
∵
，
共线
∴y=0，
=z
由\o\ac(○，1)\o\ac(○，2)，解得x=
， y=0， z=
∴M点的坐标为(
， 0，
)，
=(-
， 1， -
)，
=(-
， 0， -
)
∵
•
=
+0-
=0
∴MB⊥DP
又∵CM⊥DP
∴∠CMB为二面角B-PD-C的平面角
∵
=(-
， 0， -
)，
=(-
， 1， -
)，∴cos∠CMB=
=
∴二面角B-PD-C的大小为arccos
．
（Ⅲ）设点B到平面PAD的距离为h
∵AB⊥BC
∴AC=
=
∵PC⊥平面ABCD
∴PC⊥AC
∴PA=
=
在直角梯形ABCD中，AB=1，BC=1，CD=2
∴AD=
=
在△PAD中，∵AD=
，PA=
， PD=
∴AD2+PA2=PD2
∴∠PAD=90°
∴△PAD的面积S△PAD=
AD•PA=
∵三棱锥B-PAD的体积VB-PAD=VP-ABD
∴
•S△PAD•h=
•S△ABD•PC，
即
×h=(
×1×1)×1，解得h=
∴点B到平面PAD的距离为
．
解：（Ⅰ）证明：∵在△PBC中，BC=PC=1， PB=| 2 |
∴BC2+PC2=PB2
∴∠PCB=90°，即PC⊥BC
∵AB⊥PC
∵AB∩BC=B
∴PC⊥平面ABCD．
（Ⅱ）方法一：由（Ⅰ）知PC⊥BC
又∵BC⊥CD，PC∩CD=C
∴BC⊥平面PCD
过C作CM⊥PD于M，连接BM
∴CM是BM在平面PCD内的射影
∴BM⊥PD，
又∵CM⊥PD
∴∠CMB为二面角B-PD-C的平面角．
在△PCD中，∠PCD=90°，PC=1，CD=2，∴PD=
| PC2+CD2 |
| 5 |
又∵CM⊥PD∴PD•CM=PC•CD，∴CM=
| PC•CD |
| PD |
2
| ||
| 5 |
在△CMB中，∠BCM=90°，BC=1，CM=
2
| ||
| 5 |
∴tan∠CMB=
| BC |
| CM |
| ||
| 2 |
∴二面角B-PD-C的大小为arctan
| ||
| 2 |
方法二：如图，在平面ABCD内，以C为原点，CD、CB、CP分别为x、y、z轴，建立空间直角坐标系C-xyz，
则C（0，0，0），B（0，1，0），D（2，0，0），P（0，0，1），A（1，1，0）
过C作CM⊥DP于M，连接BM，设M（x，y，z）
则
| MC |
| DM |
| DP |
∵| MC |
| DP |
∴
| MC |
| DP |
∵
| DM |
| DP |
∴y=0，
| x-2 |
| -2 |
由\o\ac(○，1)\o\ac(○，2)，解得x=
| 2 |
| 5 |
| 4 |
| 5 |
∴M点的坐标为(
| 2 |
| 5 |
| 4 |
| 5 |
| MB |
| 2 |
| 5 |
| 4 |
| 5 |
| MC |
| 2 |
| 5 |
| 4 |
| 5 |
∵
| MB |
| DP |
| 4 |
| 5 |
| 4 |
| 5 |
∴MB⊥DP
又∵CM⊥DP
∴∠CMB为二面角B-PD-C的平面角
∵
| MC |
| 2 |
| 5 |
| 4 |
| 5 |
| MB |
| 2 |
| 5 |
| 4 |
| 5 |
| ||||
|
|
| 2 |
| 3 |
∴二面角B-PD-C的大小为arccos
| 2 |
| 3 |
（Ⅲ）设点B到平面PAD的距离为h
∵AB⊥BC
∴AC=
| AB2+BC2 |
| 2 |
∵PC⊥平面ABCD
∴PC⊥AC
∴PA=
| AC2+PC2 |
| 3 |
在直角梯形ABCD中，AB=1，BC=1，CD=2
∴AD=
| BC2+(CD-AB)2 |
| 2 |
在△PAD中，∵AD=
| 2 |
| 3 |
| 5 |
∴AD2+PA2=PD2
∴∠PAD=90°
∴△PAD的面积S△PAD=
| 1 |
| 2 |
| ||
| 2 |
∵三棱锥B-PAD的体积VB-PAD=VP-ABD
∴
| 1 |
| 3 |
| 1 |
| 3 |
即
| ||
| 2 |
| 1 |
| 2 |
| ||
| 6 |
∴点B到平面PAD的距离为
| ||
| 6 |
点评：本题主要考察了线面垂直的证明，二面角的求解，点到面的距离的计算．解题的关键是第一问要根据题中数据得出PC⊥BC而第二问可采用几何法（关键是找到垂线然后利用三垂线定理即可做出二面角的平面角）也可采用空间向量的方法证明∠CMB为二面角B-PD-C的平面角，对于第三问中点到面的距离的求解常采用轮换三棱锥的顶点但体积不变即“等积法”求解！
练习册系列答案
相关题目