题目内容
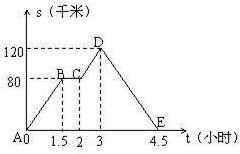 如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为
| 80 |
| 3 |
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:本题主要考查了函数图象上特殊点的实际意义,根据图象上的特殊点的实际意义即可作出判断.
解答:解:由图象可知,汽车走到距离出发点120千米的地方后又返回出发点,所以汽车共行驶了240千米,①错;
从1.5时开始到2时结束,时间在增多,而路程没有变化,说明此时在停留,停留了2-1.5=0.5小时,②对;
汽车用4.5小时走了240千米,平均速度为;240÷4.5=
千米/时,③错.
汽车自出发后3小时至4.5小时,图象是直线形式,说明是在匀速前进,④错.
故选A.
从1.5时开始到2时结束,时间在增多,而路程没有变化,说明此时在停留,停留了2-1.5=0.5小时,②对;
汽车用4.5小时走了240千米,平均速度为;240÷4.5=
| 160 |
| 3 |
汽车自出发后3小时至4.5小时,图象是直线形式,说明是在匀速前进,④错.
故选A.
点评:本题考查由图象理解对应函数关系及其实际意义,注意总路程应包括往返路程,平均速度=总路程÷总时间.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
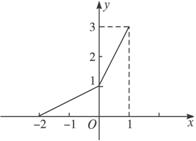
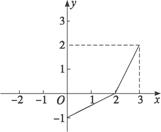
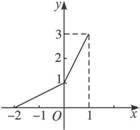
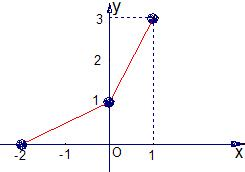 在同一平面直角坐标系中,函数y=f(x)和y=g(x)的图象关于直线y=x对称.现将y=g(x)的图象沿x轴向左平移2个单位,再沿y轴向上平移1个单位,所得的图象是由两条线段组成的折线(如图所示),则函数f(x)的表达式为( )
在同一平面直角坐标系中,函数y=f(x)和y=g(x)的图象关于直线y=x对称.现将y=g(x)的图象沿x轴向左平移2个单位,再沿y轴向上平移1个单位,所得的图象是由两条线段组成的折线(如图所示),则函数f(x)的表达式为( )A、f(x)=
| |||||||
B、f(x)=
| |||||||
C、f(x)=
| |||||||
D、f(x)=
|
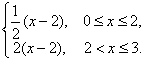 B.f(x)=
B.f(x)=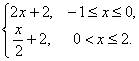
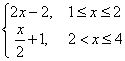 D.f(x)=
D.f(x)=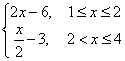
 B.f(x)=
B.f(x)=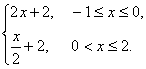
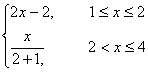 D.f(x)=
D.f(x)=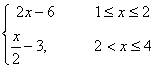
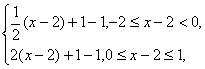 B.f(x)=
B.f(x)=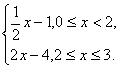
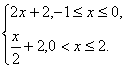 D.f(x)=
D.f(x)=