��Ŀ����
��b��0,��Բ����Ϊ
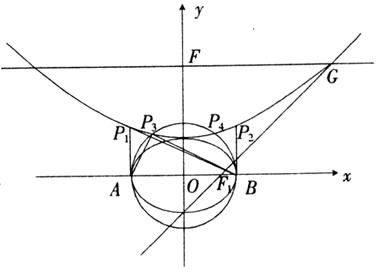
ͼ6
(1)��������������Բ���̺������߷���.
(2)��A��B�ֱ�����Բ��������Ҷ˵�,��̽�������������Ƿ���ڵ�P,ʹ�á�ABPΪֱ��������?������,��ָ�����м��������ĵ�?��˵������(���ؾ��������Щ�������).
������Ҫ������Բ�������ߵĸ���,��Բ�������ߵķ��̵Ȼ���֪ʶ,���ν�ϵ���ѧ˼���뷽��,�Լ������������.
�⣺(1)��x2=8(y-b)��y=![]() +b.
+b.
��y=b+2ʱ,x=��4,
��G�������Ϊ(4,b+2).
����������x2=8(y-b)�ڵ�G�����ߵ�l��б��k=![]() =1,
=1,
����l�ķ���Ϊy=x+b-2.
����Բ���̵�F1�������Ϊ(b,0)��
������l������Բ���ҽ���F1
����0=b+b-2,���b=1.
���������������Բ���̺������߷��̷ֱ�Ϊ![]() +y2=1��x2=8(y-1).
+y2=1��x2=8(y-1).
(2)�������ϴ��ڵ�P��ʹ�á�ABPΪֱ�������Σ������ĵ㹲��4��.

�ٷֱ��A��B��x��Ĵ��ߣ��������߷ֱ�������P1��-![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() �������ABP1�͡�ABP2����ֱ��������.
�������ABP1�͡�ABP2����ֱ��������.
����ԭ��Ϊ���ģ�![]() |AB|=
|AB|=![]() Ϊ�뾶��Բ�ܣ�����Բ�ܰ뾶
Ϊ�뾶��Բ�ܣ�����Բ�ܰ뾶![]() ������Բ�İ���᳤1������Բ�������߽�����һ�㣬��������Բ�ܱ����������ཻ������P3��P4.
������Բ�İ���᳤1������Բ�������߽�����һ�㣬��������Բ�ܱ����������ཻ������P3��P4.
���ABP3�͡�ABP4����ֱ��������.
��ΪP1A��Բ�����ڵ�A����P3��Բ���ϣ�
����P3��P1���غϣ�ͬ��P4��P2���غ�.
��P1��P2��P3��P4������������ͬ�ĵ�.