题目内容
9. 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG,且AC=1,AB=ED=EF=2,AD=DG=4.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG,且AC=1,AB=ED=EF=2,AD=DG=4.(1)求证:BE⊥平面DEFG;
(2)求证:BF∥平面ACGD;
(3)求三棱锥A-FBC的体积.
分析 (1)由于平面ABC∥平面DEFG得AB∥DE,由AB=ED得四边形ABED是平行四边形,故BE∥AD,再由AD⊥平面DEFG得到BE⊥平面DEFG;
(2)取DG中点H,连接AH,FH,易证四边形ABFH是平行四边形,得出BF∥AH,从而得到BF∥平面ACGD;
(3)由平面ABC∥平面DEFG,AD⊥平面DEFG可知AD⊥平面ABC,于是V棱锥A-FBC=V棱锥F-ABC=$\frac{1}{3}$S△ABC•AD.
解答  证明:(1)∵平面ABC∥平面DEFG,平面ABED∩平面ABC=AB,平面ABED∩平面DEFG=DE,
证明:(1)∵平面ABC∥平面DEFG,平面ABED∩平面ABC=AB,平面ABED∩平面DEFG=DE,
∴AB∥DE,又∵AB=ED,
∴四边形ABED是平行四边形,
∴BE∥AD,∵AD⊥平面DEFG,
∴:BE⊥平面DEFG.
(2)取DG中点H,连接AH,FH.
则DH=$\frac{1}{2}$DG=2,∵EF∥DG,EF=2
∴EF∥DH,EF=DH,
∴四边形DEFG是平行四边形,
∴FH∥DE,FH=DE.
由(1)证明可知四边形ABED是平行四边形,
∴AB∥DE,AB=DE,
∴AB∥FH,AB=FH,
∴四边形ABFH是平行四边形,
∴BF∥AH,又∵AH?平面ACGD,BF?平面ACGD,
∴BF∥平面ACGD.
(3)∵平面ABC∥平面DEFG,AD⊥平面DEFG,
∴AD⊥平面ABC,
∴V棱锥A-FBC=V棱锥F-ABC=$\frac{1}{3}$S△ABC•AD=$\frac{1}{3}$×$\frac{1}{2}$×2×1×4=$\frac{4}{3}$.
点评 本题考查了线面垂直,线面平行的判定和几何体的体积计算,寻找直线平行与垂直的关系是解题关键.

练习册系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的体积为( )
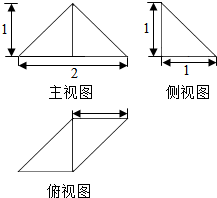

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
1.设集合A={x|x≥3},B={x|x≤3},则A∩B=( )
| A. | ∅ | B. | R | C. | {x||x≤3} | D. | {3} |
10.若集合A={y|y=2x},B={x|x2-2x-3>0,x∈R},那么A∩B=( )
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (0,-1)∪(3,+∞) |