题目内容
将1，2，3，…，9这九个数字平均分成三组，则每组的三个数都成等差数列的概率是
．
| 1 |
| 56 |
| 1 |
| 56 |
分析：先把9个数分成3组，根据排列组合的性质可求得所有的组的数，然后把三个数成等差数列的组，分别枚举出来，
可知共有5组，然后利用概率的性质求得答案．
可知共有5组，然后利用概率的性质求得答案．
解答：解：9个数分成三组，共有组
=8×7×5 组，其中每组的三个数均成等差数列，有
{（1，2，3），（4，5，6），（7，8，9）}、{（1，2，3），（4，6，8），（5，7，9）}、
{（1，3，5），（2，4，6），（7，8，9）}、{（1，4，7），（2，5，8），（3，6，9）}、
{（1，5，9），（2，3，4），（6，7，8）}，共5组．
∴所求概率为
=
．
故答案为：
．
| ||||||
|
{（1，2，3），（4，5，6），（7，8，9）}、{（1，2，3），（4，6，8），（5，7，9）}、
{（1，3，5），（2，4，6），（7，8，9）}、{（1，4，7），（2，5，8），（3，6，9）}、
{（1，5，9），（2，3，4），（6，7，8）}，共5组．
∴所求概率为
| 5 |
| 8×7×5 |
| 1 |
| 56 |
故答案为：
| 1 |
| 56 |
点评：本题主要考查了等差关系的确定和概率的性质，对于数量比较小的问题中，可以用枚举的方法解决问题．
练习册系列答案
阅读快车系列答案
相关题目
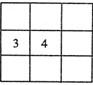12、将1，2，3，，9这9个数字填在如图的9个空格中，要求每一行从左到右，每一列从上到下分别依次增大，当3，4固定在图中的位置时，填写空格的方法数为（ ）
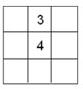15、将1、2、3、…、9这九个数字填在如图所示的9个空格中，要求每一行
（2008•和平区三模）将1，2，3，…9，这9个数填在如图的9个空格中，要求每一行从左到右，每一列从上到下依次增大，当3，4固定在图中位置时，所填写空格的方法有（ ）