题目内容
设集合A={（x，y）|x+y≥1}，B={（x，y）|x≤2且y≤2}，若（x，y）∈A∩B，且kx+y的最大值是6，则实数k的值为
2或-4
2或-4
．分析：先作出集合A表示的平面区域，令z=kx+y，则可得y=-kx+z，则z为直线在y轴上的截距，截距越大，z越大，结合图象分①若k=0；②-k＞0．③-k＜0三种情况分别判断kx+y取得最大值的条件，从而可求k
解答：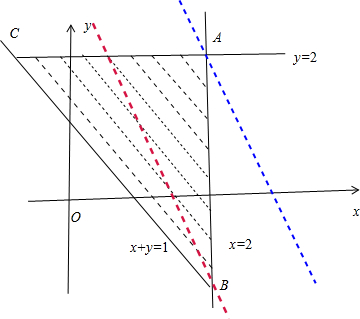
解：作出集合A表示的平面区域，如图所示的阴影部分
令z=kx+y，则可得y=-kx+z，则z为直线在y轴上的截距，截距越大，z越大
由题意可得A（2，2），B（2，-1），C（-1，2）
①若k=0，则y=z的最大值为2，不符合题意
②若-k＞0．则y=-kx+z在C（-1，2）取得最大值，此时有k+2=6，
∴k=-4，不符合题意
③若-k＜0，则y=-kx+z在C（2，2）取得最大值，此时有2k+2=6，
∴k=2
综上可得k=2或k=-4
故答案为：2或-4
解：作出集合A表示的平面区域，如图所示的阴影部分令z=kx+y，则可得y=-kx+z，则z为直线在y轴上的截距，截距越大，z越大
由题意可得A（2，2），B（2，-1），C（-1，2）
①若k=0，则y=z的最大值为2，不符合题意
②若-k＞0．则y=-kx+z在C（-1，2）取得最大值，此时有k+2=6，
∴k=-4，不符合题意
③若-k＜0，则y=-kx+z在C（2，2）取得最大值，此时有2k+2=6，
∴k=2
综上可得k=2或k=-4
故答案为：2或-4
点评：本题主要考查了利用约束条件求解目标函数的最大值，解题的关键需要判断直线的斜率-k的范围以确定取得最大值的位置，体现了分类讨论思想的应用
练习册系列答案
阅读快车系列答案
相关题目
设集合A=B={（x，y）|x∈R，y∈R}，从A到B的映射f：（x，y）→（x+2y，2x-y），则在映射f下B中的元素（1，1）对应的A中元素为（ ）
| A、（1，3） | ||||
| B、（1，1） | ||||
C、(
| ||||
D、(
|
