题目内容
设集合A=B={(x,y)|x∈R,y∈R},从A到B的映射f:(x,y)→(x+2y,2x-y),则在映射f下B中的元素(1,1)对应的A中元素为
(
,
)
| 3 |
| 5 |
| 1 |
| 5 |
(
,
)
.| 3 |
| 5 |
| 1 |
| 5 |
分析:根据两个集合之间的对应关系,写出B集合与所给的(1,1)对应的关于x,y的方程组,解方程组即可.
解答:解:∵从A到B的映射f:(x,y)→(x+2y,2x-y),
∴在映射f下B中的元素(1,1)对应的A的元素满足x+2y=1,2x-y=1
解得x=
,y=
则在映射f下B中的元素(1,1)对应的A中元素为 (
,
)
故答案为:(
,
).
∴在映射f下B中的元素(1,1)对应的A的元素满足x+2y=1,2x-y=1
解得x=
| 3 |
| 5 |
| 1 |
| 5 |
则在映射f下B中的元素(1,1)对应的A中元素为 (
| 3 |
| 5 |
| 1 |
| 5 |
故答案为:(
| 3 |
| 5 |
| 1 |
| 5 |
点评:本题考查映射,本题解题的关键是看出两个集合的对应的关系,写出两个集合对应的变量的关系式,本题是一个基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 , B=
, B= , 函数f(x)=
, 函数f(x)=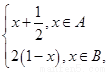 若x
若x
 , 且
, 且 ,则x
,则x B.
B. C.
C. D.
D.
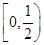 ,
B=
,
B= ,
函数f(x)=
,
函数f(x)= 若
若 ,
且
,
且 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 ,
B=
,
B= ,
函数f(x)=
,
函数f(x)=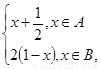 若x
若x
 ,
且f [ f (x
,
且f [ f (x B.
B. C.
C. D.
D.
 ,
B=
,
B= ,
函数f(x)=
,
函数f(x)=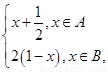 若x
若x
 ,
且f [ f (x
,
且f [ f (x B.
B. C.
C. D.
D.
 若x
若x