题目内容
如图，在棱锥P－ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC＝60°，M为PB的中点．
(1)求证：PA⊥CD；
(2)求二面角P－AB－D的大小；
(3)求三棱锥B－CDM的体积．
答案：
解析：
解析：
|
(1)取DC的中点H，连结PH，AH，∵△PDC、△ADC均为正三角形，∴DC⊥PH，DC⊥AH，∴DC⊥平面PHA，∴DC⊥PA． (2) 在△PAH中，∵易证PH⊥AH，且PH＝AH，∴∠PAH＝45°． 故二面角P－AB－D的度数为45°． (3) |
．
．
练习册系列答案
相关题目
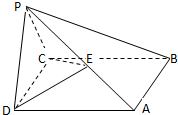如图，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，底面ABCD是菱形，且∠ADC=60°，E为PA的中点，二面角P-CD-A为120°．
如图，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC=60°，M为PB的中点，
如图，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC=60°，M为PB的中点，
