题目内容
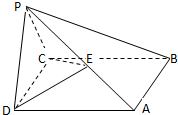 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,且∠ADC=60°,E为PA的中点,二面角P-CD-A为120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,且∠ADC=60°,E为PA的中点,二面角P-CD-A为120°.(1)求证:PA⊥平面CDE;
(2)求二面角P-AB-D的大小.
分析:(1)取CD中点G,连接PG,AG.利用等腰三角形的性质和线面垂直的判定定理可证明CD⊥平面PAG,可得CD⊥PA;再证明DE⊥PA即可.
(2))利用CD⊥平面PAG,可得∠PGA是二面角P-CD-A的平面角,即∠PGA=120°.再利用菱形的性质和三垂线定理及其逆定理可证∠PAG是二面角P-AB-D的平面角,求出即可.
(2))利用CD⊥平面PAG,可得∠PGA是二面角P-CD-A的平面角,即∠PGA=120°.再利用菱形的性质和三垂线定理及其逆定理可证∠PAG是二面角P-AB-D的平面角,求出即可.
解答:证明:(1)取CD中点G,连接PG,AG.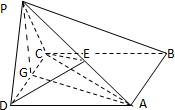
∵侧面PDC是边长为2的正三角形,∴PG⊥CD,
∵底面ABCD是菱形,∠ADC=60°,
∴△DAC也是边长为2的正三角形,∴GA⊥CD,
∴CD⊥平面PAG,∴PA⊥CD,
在△PDA中,PD=AD,E为PA的中点,∴PA⊥DE.
又CD∩DE=D,∴PA⊥平面CDE.
(2)∵CD⊥平面PAG,∴∠PGA是二面角P-CD-A的平面角,∴∠PGA=120°.
又∵底面ABCD是菱形,
∴AB∥CD,∴AB⊥平面PAG,
平面PAG∩平面ABD=AG,平面PAG∩平面PAB=AP.
∴∠PAG是二面角P-AB-D的平面角,
∵PD=AD,∴Rt△PDG≌Rt△AGD,PG=AG,∠PAG=30°,
∴二面角P-AB-D为30°.

∵侧面PDC是边长为2的正三角形,∴PG⊥CD,
∵底面ABCD是菱形,∠ADC=60°,
∴△DAC也是边长为2的正三角形,∴GA⊥CD,
∴CD⊥平面PAG,∴PA⊥CD,
在△PDA中,PD=AD,E为PA的中点,∴PA⊥DE.
又CD∩DE=D,∴PA⊥平面CDE.
(2)∵CD⊥平面PAG,∴∠PGA是二面角P-CD-A的平面角,∴∠PGA=120°.
又∵底面ABCD是菱形,
∴AB∥CD,∴AB⊥平面PAG,
平面PAG∩平面ABD=AG,平面PAG∩平面PAB=AP.
∴∠PAG是二面角P-AB-D的平面角,
∵PD=AD,∴Rt△PDG≌Rt△AGD,PG=AG,∠PAG=30°,
∴二面角P-AB-D为30°.
点评:本题考查了等腰三角形的性质和线面垂直的判定定理、菱形的性质和三垂线定理及其逆定理、二面角的作法和求值等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ADC=60°,M为PB的中点,
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ADC=60°,M为PB的中点, 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ADC=60°,M为PB的中点,
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ADC=60°,M为PB的中点,
