题目内容
已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y2-6y+8≤0},
若A∩B≠φ,则实数a的取值范围为_________.
若A∩B≠φ,则实数a的取值范围为_________.
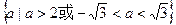
由题知可解得A={y|y>a2+1或y<a}, B={y|2≤y≤4},我们不妨先考虑当A∩B=φ时a的范围.
如图 由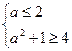 ,得
,得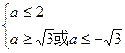
∴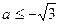 或
或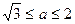 .
.
即A∩B=φ时a的范围为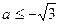 或
或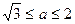 .而A∩B≠φ时a的范围显然是其补集,从而所求范围为
.而A∩B≠φ时a的范围显然是其补集,从而所求范围为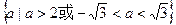 .
.
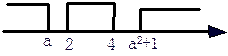 |
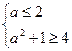 ,得
,得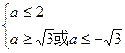
∴
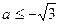 或
或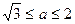 .
.即A∩B=φ时a的范围为
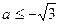 或
或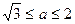 .而A∩B≠φ时a的范围显然是其补集,从而所求范围为
.而A∩B≠φ时a的范围显然是其补集,从而所求范围为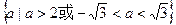 .
.
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
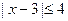 }, N={
}, N={ }, 则 M
}, 则 M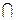 N =" " ( )
N =" " ( )
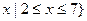
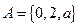 ,
,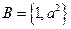 ,若
,若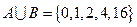 ,则
,则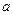 的值为( )
的值为( )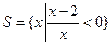 ,
,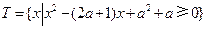
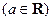 ,若
,若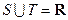 ,则实数
,则实数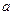 的取值范围是( )
的取值范围是( )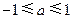
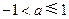
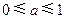
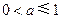
 ,则
,则 等于
等于




 的定义域为A,函数y=2-|x|值域为B,则( )
的定义域为A,函数y=2-|x|值域为B,则( ) B
B

 ,
, ,则
,则 .
.