题目内容
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为
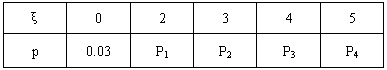
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
解:(1)设该同学在A处投中为事件A,在B处投中为事件B,
则事件A,B相互独立,且P(A)=0.25,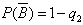 ,P(B)=q2,
,P(B)=q2,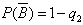 ,
,
根据分布列知:ξ=0时, =0.03,
=0.03,
所以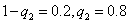 ;
;
(2)当ξ=2时,P1=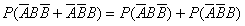 =0.75q2(
=0.75q2(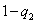 )×2=1.5q2(
)×2=1.5q2(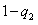 )=0.24,
)=0.24,
当ξ=3时,P2=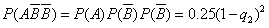 =0.01,
=0.01,
当ξ=4时,P3=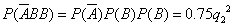 =0.48,
=0.48,
当ξ=5时,P4=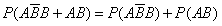
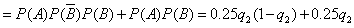 =0.24,
=0.24,
所以随机变量ξ的分布列为
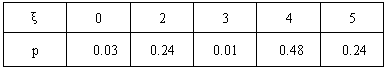
随机变量ξ的数学期望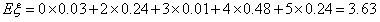 。
。
(3)该同学选择都在B处投篮得分超过3分的概率为

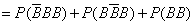
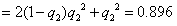 ,
,
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72,
由此看来该同学选择都在B处投篮得分超过3分的概率大。
则事件A,B相互独立,且P(A)=0.25,
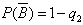 ,P(B)=q2,
,P(B)=q2,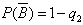 ,
,根据分布列知:ξ=0时,
 =0.03,
=0.03,所以
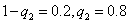 ;
;(2)当ξ=2时,P1=
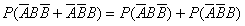 =0.75q2(
=0.75q2(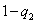 )×2=1.5q2(
)×2=1.5q2(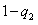 )=0.24,
)=0.24,当ξ=3时,P2=
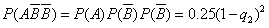 =0.01,
=0.01,当ξ=4时,P3=
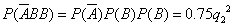 =0.48,
=0.48,当ξ=5时,P4=
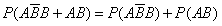
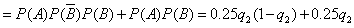 =0.24,
=0.24,所以随机变量ξ的分布列为
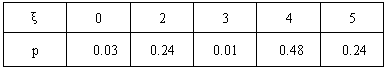
随机变量ξ的数学期望
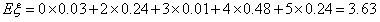 。
。(3)该同学选择都在B处投篮得分超过3分的概率为

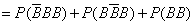
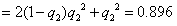 ,
,该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72,
由此看来该同学选择都在B处投篮得分超过3分的概率大。

练习册系列答案
相关题目
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
| ξ | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.