题目内容
18.已知函数f(x)=ax3+bx2+cx+1(a<0)的导数f′(x)满足下列条件:当1<x<4时,f′(x)>0;当x>4或x<1时,f′(x)<0;当x=4或x=1时,f′(x)=0.(1)试画出函数f(x)的图象;
(2)若f(x)的图象与x轴有两个交点,求a的值.
分析 (1)先求出函数的单调区间,从而画出函数的大致图象;(2)由题意得到方程组,解出a的值即可.
解答 解:(1)由题意得:f(x)在(-∞,1)递减,在(1,4)递增,在(4,+∞)递减,
且f(0)=1,
画出函数f(x)的大致图象,如图示: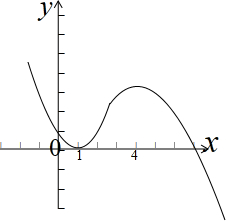 ;
;
(2)由f(x)的图象与x轴有两个交点,
得:f′(1)=0,f(1)=0,f′(4)=0,
即$\left\{\begin{array}{l}{a+b+c+1=0}\\{3a+2b+c=0}\\{48a+8b+c=0}\end{array}\right.$,解得:a=-$\frac{3}{17}$.
点评 本题考查了函数的单调性,考查导数的应用,考查函数的极值问题,是一道中档题.

练习册系列答案
相关题目
8. 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
(1)求证:GH∥平面CDE;
(2)求证:BC⊥平面CDE;
(3)求三棱锥A-BCG的体积.
 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.(1)求证:GH∥平面CDE;
(2)求证:BC⊥平面CDE;
(3)求三棱锥A-BCG的体积.
12.在空间中,下列结论正确的是( )
| A. | 平行于同一直线的两直线平行 | B. | 垂直于同一直线的两直线平行 | ||
| C. | 平行于同一平面的两直线平行 | D. | 垂直于同一平面的两直线垂直 |
 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),连结MC,MB,OT.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),连结MC,MB,OT.