题目内容
海事救护船A在基地的北偏东60°，与基地相距20
海里，渔船B被困海面，已知B距离基地20海里，而且在救护船A正西方，则渔船B与救护船A的距离是 ．
| 3 |
分析：先根据正弦定理求得sinB的值，进而确定B的值，最后根据B的值，求得AB．
解答：解：设基地为O处，根据正弦定理可知
=
，
∴sinB=
=
=
∴B=60°或120°
当B=60°，∠BOA=90°，∠A=30°，BA=2OB=40
当B=120°，∠A=∠B=30°，
∴OB=AB=20
故渔船B与救护船A的距离是20或40海里．
故答案为：20或40海里．
| OB |
| sinA |
| OA |
| sinB |
∴sinB=
| OAsinA |
| OB |
20
| ||||
| 20 |
| ||
| 2 |
∴B=60°或120°
当B=60°，∠BOA=90°，∠A=30°，BA=2OB=40
当B=120°，∠A=∠B=30°，
∴OB=AB=20
故渔船B与救护船A的距离是20或40海里．
故答案为：20或40海里．
点评：本题主要考查了解三角形的实际应用，考查学生转化和化归思想和逻辑思维的能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
海事救护船A在基地的北偏东60°，与基地相距100
海里，渔船B被困海面，已知B距离基地100海里，而且在救护船A正西方，则渔船B与救护船A的距离是（ ）
| 3 |
| A、100海里 | ||
| B、200海里 | ||
| C、100海里或200海里 | ||
D、100
|
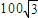海里，渔船B被困海面，已知B距离基地100海里，而且在救护船A正西方，则渔船B与救护船A的距离是（ ）
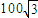海里
海里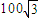，渔船B被困海面，已知B距离基地100海里，而且在救护船A正西方，则渔船B与救护船A的距离是（ ）
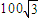海里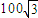
海里，渔船B被困海面，已知B距离基地100海里，而且在救护船A正西方，则渔船B与救护船A的距离是（ ）
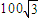海里