题目内容
(2009年)若函数y=
ax3-
ax2-2ax(a≠0)在[-1,2]上为增函数,则实数a的取值范围是
| 1 |
| 3 |
| 1 |
| 2 |
a<0
a<0
.分析:求出导函数,将已知条件转化为ax2-ax-2a≥0在[-1,2]上恒成立,结合二次函数的图象得到a的范围.
解答:解:y′=ax2-ax-2a,
因为函数y=
ax3-
ax2-2ax(a≠0)在[-1,2]上为增函数,
所以ax2-ax-2a≥0在[-1,2]上恒成立,
即a(x-2)(x+1)≥0在[-1,2]上恒成立,
所以a<0,
故答案为:a<0.
因为函数y=
| 1 |
| 3 |
| 1 |
| 2 |
所以ax2-ax-2a≥0在[-1,2]上恒成立,
即a(x-2)(x+1)≥0在[-1,2]上恒成立,
所以a<0,
故答案为:a<0.
点评:本题考查导函数的符号与函数单调性的关系,若已知函数的单调性求函数的参数的范围,应该令导函数大于等于(小于等于)0恒成立,属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
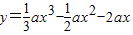 (a≠0)在[-1,2]上为增函数,则实数a的取值范围是 .
(a≠0)在[-1,2]上为增函数,则实数a的取值范围是 .