题目内容
有这样一道题:“在△ABC中,已知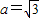 ,
,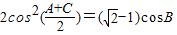 ,求角A.”已知该题的答案是A=60°,若横线处的条件为三角形中某一边的长度,则此条件应为 .
,求角A.”已知该题的答案是A=60°,若横线处的条件为三角形中某一边的长度,则此条件应为 .
【答案】分析:由已知条件根据倍角公式及诱导公式,可求出B=45°,再由A=60°可得C=75°,进而利用正弦定理可求出b=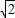 ,
,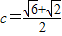 ,再由b=
,再由b= 时,三角形有两解,可得答案.
时,三角形有两解,可得答案.
解答:解:在△ABC中,A+B+C=π
∴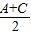 =
= -
-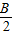
∴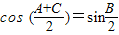
∴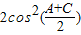 =1-cosB=
=1-cosB=
即cosB=
B=45°
由A=60°可得C=75°
再由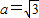 ,
,
可得b=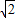 ,
,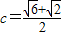
又∵b=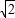 时,三角形有两解
时,三角形有两解
故答案为: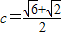
点评:本题考查的知识点是解三角形,其中易忽略b=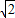 时,三角形有两解,而错解为b=
时,三角形有两解,而错解为b=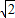 或
或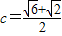
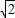 ,
,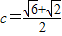 ,再由b=
,再由b= 时,三角形有两解,可得答案.
时,三角形有两解,可得答案.解答:解:在△ABC中,A+B+C=π
∴
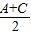 =
= -
-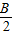
∴
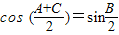
∴
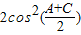 =1-cosB=
=1-cosB=
即cosB=

B=45°
由A=60°可得C=75°
再由
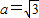 ,
,可得b=
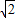 ,
,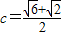
又∵b=
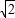 时,三角形有两解
时,三角形有两解故答案为:
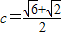
点评:本题考查的知识点是解三角形,其中易忽略b=
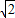 时,三角形有两解,而错解为b=
时,三角形有两解,而错解为b=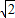 或
或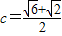

练习册系列答案
相关题目
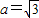 ,
,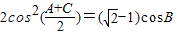 ,求角A.”已知该题的答案是A=60°,若横线处的条件为三角形中某一边的长度,则此条件应为 .
,求角A.”已知该题的答案是A=60°,若横线处的条件为三角形中某一边的长度,则此条件应为 .