题目内容
(Ⅰ)设x≥1,y≥1,证明x+y+| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
(Ⅱ)1≤a≤b≤c,证明logab+logbc+logca≤logba+logcb+logac.
分析:(Ⅰ)根据题意,首先对原不等式进行变形有x+y+
≤
+
+xy?xy(x+y)+1≤x+y+(xy)2;再用做差法,让右式-左式,通过变形、整理化简可得右式-左式=(xy-1)(x-1)(y-1),又由题意中x≥1,y≥1,判断可得右式-左式≥0,从而不等式得到证明.
(Ⅱ)首先换元,设logab=x,logbc=y,由换底公式可得:logba=
,logcb=
,logac=
,logac=xy,将其代入要求证明的不等式可得:x+y+
≤
+
+xy;又有logab=x≥1,logbc=y≥1,借助(Ⅰ)的结论,可得证明.
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
(Ⅱ)首先换元,设logab=x,logbc=y,由换底公式可得:logba=
| 1 |
| x |
| 1 |
| y |
| 1 |
| xy |
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
解答:证明:(Ⅰ)由于x≥1,y≥1;则x+y+
≤
+
+xy?xy(x+y)+1≤x+y+(xy)2;
用作差法,右式-左式=(x+y+(xy)2)-(xy(x+y)+1)
=((xy)2-1)-(xy(x+y)-(x+y))
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1);
又由x≥1,y≥1,则xy≥1;即右式-左式≥0,从而不等式得到证明.
(Ⅱ)设logab=x,logbc=y,
由换底公式可得:logba=
,logcb=
,logca=
,logac=xy,
于是要证明的不等式可转化为x+y+
≤
+
+xy;
其中logab=x≥1,logbc=y≥1,
由(Ⅰ)的结论可得,要证明的不等式成立.
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
用作差法,右式-左式=(x+y+(xy)2)-(xy(x+y)+1)
=((xy)2-1)-(xy(x+y)-(x+y))
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1);
又由x≥1,y≥1,则xy≥1;即右式-左式≥0,从而不等式得到证明.
(Ⅱ)设logab=x,logbc=y,
由换底公式可得:logba=
| 1 |
| x |
| 1 |
| y |
| 1 |
| xy |
于是要证明的不等式可转化为x+y+
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
其中logab=x≥1,logbc=y≥1,
由(Ⅰ)的结论可得,要证明的不等式成立.
点评:本题考查不等式的证明,要掌握不等式证明常见的方法,如做差法、放缩法;其次注意(Ⅱ)证明在变形后用到(Ⅰ)的结论,这个高考命题考查转化思想的一个方向.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
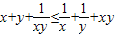 .
.