题目内容
设x≥1,y≥1,证明:x+y+
≤
+
+xy.
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
证明:要证x+y+
≤
+
+xy,
只需证明
-
-
≤xy-x-y,
只需证明(1-
)(1-
)≤(1-x)(1-y)=(x-1)(y-1),
只需证明1-
≤x-1;1-
≤y-1,
即证x+
≥2,y+
≥2,(x≥1,y≥1)这是均值不等式,
所以x≥1,y≥1,x+y+
≤
+
+xy得证.
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
只需证明
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |
只需证明(1-
| 1 |
| x |
| 1 |
| y |
只需证明1-
| 1 |
| x |
| 1 |
| y |
即证x+
| 1 |
| x |
| 1 |
| y |
所以x≥1,y≥1,x+y+
| 1 |
| xy |
| 1 |
| x |
| 1 |
| y |

练习册系列答案
相关题目
 中,
中, 平面
平面 ,底面
,底面 .
. 时,求证:
时,求证: ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.


 ,
, ………………2分
………………2分 ,得证。
,得证。 ,只要
,只要
 ,即
,即 ………6分
………6分
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以

 ………………3分
………………3分
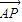 =
=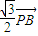 ,|
,| |=2+
|=2+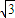 .
.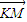 •
•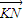 =0,试证:直线MN必过x轴上的定点.
=0,试证:直线MN必过x轴上的定点.