题目内容
正实数x1,x2及函数f(x)满足4x=| 1+f(x) | 1-f(x) |
分析:先解出f(x) 的解析式,根据f(x1)+f(x2)=1 可得,4(x1+x2)-3=4x1+4x2,再使用基本不等式可求得
4(x1+x2)≥9,由此求得f(x1+x2)=1-
的最小值.
4(x1+x2)≥9,由此求得f(x1+x2)=1-
| 2 |
| 4x1+x2+1 |
解答:解:∵4x=
,∴f(x)=
,∵f(x1)+f(x2)=1,
∴
+
=1,通分并化为整式得
4(x1+x2)-3=4x1+4x2≥2
,即 4(x1+x2)≥2
,
两边同时除以
解得
≥2,∴4(x1+x2)≥9.
f(x1+x2)=
=1-
≥1-
=
,故答案为
.
| 1+f(x) |
| 1-f(x) |
| 4x-1 |
| 4x+1 |
∴
| 4x1-1 |
| 4x1+1 |
| 4x2-1 |
| 4x2+1 |
4(x1+x2)-3=4x1+4x2≥2
| 4 (x1+x2) |
| 4 (x1+x2) |
两边同时除以
| 4 (x1+x2) |
| 4 (x1+x2) |
f(x1+x2)=
| 4x1+x2-1 |
| 4x1+x2+1 |
| 2 |
| 4x1+x2+1 |
| 2 |
| 9+1 |
| 4 |
| 5 |
| 4 |
| 5 |
点评:本题考查求函数的解析式,指数幂的运算法则,以及基本不等式的应用,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .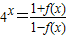 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )

 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .