题目内容
正实数x1,x2及函数f(x)满足 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .
【答案】分析:先解出f(x) 的解析式,根据f(x1)+f(x2)=1 可得, -3=
-3= +
+ ,再使用基本不等式可求得
,再使用基本不等式可求得
 ≥9,由此求得f(x1+x2)=1-
≥9,由此求得f(x1+x2)=1- 的最小值.
的最小值.
解答:解:∵ ,∴f(x)=
,∴f(x)= ,∵f(x1)+f(x2)=1,
,∵f(x1)+f(x2)=1,
∴ +
+ =1,通分并化为整式得
=1,通分并化为整式得
 -3=
-3= +
+ ≥2
≥2  ,解得
,解得  ≥3,
≥3,
∴ ≥9,
≥9,
f(x1+x2)= =1-
=1- ≥1-
≥1- =
= ,故答案为
,故答案为  .
.
点评:本题考查求函数的解析式,指数幂的运算法则,以及基本不等式的应用.
 -3=
-3= +
+ ,再使用基本不等式可求得
,再使用基本不等式可求得 ≥9,由此求得f(x1+x2)=1-
≥9,由此求得f(x1+x2)=1- 的最小值.
的最小值.解答:解:∵
 ,∴f(x)=
,∴f(x)= ,∵f(x1)+f(x2)=1,
,∵f(x1)+f(x2)=1,∴
 +
+ =1,通分并化为整式得
=1,通分并化为整式得  -3=
-3= +
+ ≥2
≥2  ,解得
,解得  ≥3,
≥3,∴
 ≥9,
≥9,f(x1+x2)=
 =1-
=1- ≥1-
≥1- =
= ,故答案为
,故答案为  .
.点评:本题考查求函数的解析式,指数幂的运算法则,以及基本不等式的应用.

练习册系列答案
相关题目
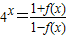 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )

 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .