题目内容
设 。
。
(1)求f(x)的表达式;
(2)设函数g(x)=ax2-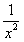 + f(x),则是否存在实数a,使得g(x)为奇函数?说明理由;
+ f(x),则是否存在实数a,使得g(x)为奇函数?说明理由;
(3)解不等式f(x)-x>2。
 。
。(1)求f(x)的表达式;
(2)设函数g(x)=ax2-
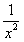 + f(x),则是否存在实数a,使得g(x)为奇函数?说明理由;
+ f(x),则是否存在实数a,使得g(x)为奇函数?说明理由;(3)解不等式f(x)-x>2。
解:(1)∵ ,
,
∴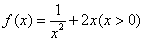 。
。
(2)∵g(x)=ax2+2x的定义域为(0,+∞),
又g(1)=2+a,g(-1)不存在,
显然g(1)≠g(-1),
∴不存在实数a,使得g(x)为奇函数。
(3)∵f(x)-x>2,
∴f(x)-x-2>0,
即 +x-2>0,有x3-2x2+1>0,
+x-2>0,有x3-2x2+1>0,
于是(x3-x2)-(x2-1)>0,
化简,得(x-1)(x2-x+1)>0,
∴(x-1)(x-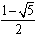 )(x-
)(x-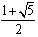 )>0,
)>0,
又x>0,
∴解得:0<x<1或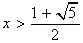 ,
,
因此原不等式的解集为{x0<x<1或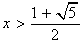 }。
}。
 ,
,∴
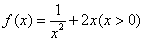 。
。(2)∵g(x)=ax2+2x的定义域为(0,+∞),
又g(1)=2+a,g(-1)不存在,
显然g(1)≠g(-1),
∴不存在实数a,使得g(x)为奇函数。
(3)∵f(x)-x>2,
∴f(x)-x-2>0,
即
 +x-2>0,有x3-2x2+1>0,
+x-2>0,有x3-2x2+1>0,于是(x3-x2)-(x2-1)>0,
化简,得(x-1)(x2-x+1)>0,
∴(x-1)(x-
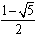 )(x-
)(x-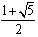 )>0,
)>0,又x>0,
∴解得:0<x<1或
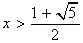 ,
,因此原不等式的解集为{x0<x<1或
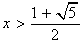 }。
}。 
练习册系列答案
相关题目
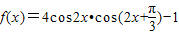 .
.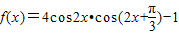 .
.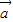 =(sinx,
=(sinx,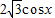 ),
),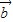 =(2sinx,sinx),设
=(2sinx,sinx),设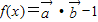 ,
, ,求f(x)的值域;
,求f(x)的值域;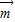 =(t,0)作长度最短的平移后,其图象关于原点对称,求
=(t,0)作长度最短的平移后,其图象关于原点对称,求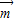 的坐标.
的坐标.