题目内容
已知向量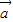 =(sinx,
=(sinx,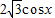 ),
),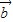 =(2sinx,sinx),设
=(2sinx,sinx),设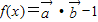 ,
,(1)求f(x)的最小正周期及单调递增区间;
(2)若
 ,求f(x)的值域;
,求f(x)的值域;(3)若f(x)的图象按
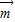 =(t,0)作长度最短的平移后,其图象关于原点对称,求
=(t,0)作长度最短的平移后,其图象关于原点对称,求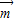 的坐标.
的坐标.
【答案】分析:(1)由已知中向量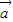 =(sinx,
=(sinx,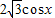 ),
),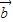 =(2sinx,sinx),设
=(2sinx,sinx),设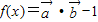 ,根据向量数量积计算公式,我们易求出f(x)的解析式,利用降幂公式(二倍角公式逆用)及辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的图象和性质,得到(x)的最小正周期及单调递增区间;
,根据向量数量积计算公式,我们易求出f(x)的解析式,利用降幂公式(二倍角公式逆用)及辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的图象和性质,得到(x)的最小正周期及单调递增区间;
(2)根据(1)中所得函数f(x)的解析式,结合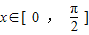 及正弦型函数的图象和性质,可求出此时f(x)的值域;
及正弦型函数的图象和性质,可求出此时f(x)的值域;
(3)f(x)的图象按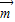 =(t,0)作长度最短的平移后,其图象关于原点对称,即此时原点是f(x)的对称中心,根据(1)中解析式,求出函数f(x)的距离原点最近的对称中心,即可得到
=(t,0)作长度最短的平移后,其图象关于原点对称,即此时原点是f(x)的对称中心,根据(1)中解析式,求出函数f(x)的距离原点最近的对称中心,即可得到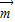 的坐标.
的坐标.
解答:解: =
=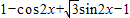 =
=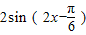 (4分)
(4分)
(1)最小正周期为: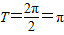
 (k∈Z)
(k∈Z)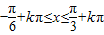 (k∈Z)
(k∈Z)
∴单调递增区间为[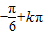 ,
,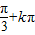 ](k∈Z)(7分)
](k∈Z)(7分)
(2)∵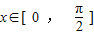 ∴
∴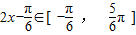
∴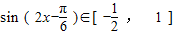 ∴f(x)∈[-1,2](10分)
∴f(x)∈[-1,2](10分)
(3)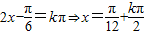 (k∈Z)
(k∈Z)
∴f(x)的对称中心坐标为(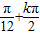 ,0)(k∈Z)
,0)(k∈Z)
∵f(x)的图象按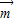 的长度最短的平移
的长度最短的平移
∴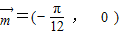 (13分)
(13分)
点评:本题考查的知识点是平面向量的数量积运算,正弦型函数的周期,单调性,最值及函数图象的平移变换,是三角函数图象和性质与平面向量的综合应用,熟练掌握正弦型函数的图象和性质是解答本题的关键.
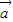 =(sinx,
=(sinx,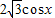 ),
),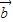 =(2sinx,sinx),设
=(2sinx,sinx),设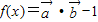 ,根据向量数量积计算公式,我们易求出f(x)的解析式,利用降幂公式(二倍角公式逆用)及辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的图象和性质,得到(x)的最小正周期及单调递增区间;
,根据向量数量积计算公式,我们易求出f(x)的解析式,利用降幂公式(二倍角公式逆用)及辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的图象和性质,得到(x)的最小正周期及单调递增区间;(2)根据(1)中所得函数f(x)的解析式,结合
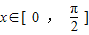 及正弦型函数的图象和性质,可求出此时f(x)的值域;
及正弦型函数的图象和性质,可求出此时f(x)的值域;(3)f(x)的图象按
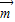 =(t,0)作长度最短的平移后,其图象关于原点对称,即此时原点是f(x)的对称中心,根据(1)中解析式,求出函数f(x)的距离原点最近的对称中心,即可得到
=(t,0)作长度最短的平移后,其图象关于原点对称,即此时原点是f(x)的对称中心,根据(1)中解析式,求出函数f(x)的距离原点最近的对称中心,即可得到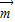 的坐标.
的坐标.解答:解:
 =
=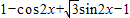 =
=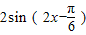 (4分)
(4分)(1)最小正周期为:
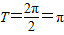
 (k∈Z)
(k∈Z)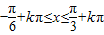 (k∈Z)
(k∈Z)∴单调递增区间为[
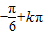 ,
,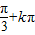 ](k∈Z)(7分)
](k∈Z)(7分)(2)∵
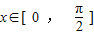 ∴
∴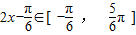
∴
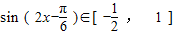 ∴f(x)∈[-1,2](10分)
∴f(x)∈[-1,2](10分)(3)
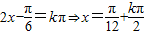 (k∈Z)
(k∈Z)∴f(x)的对称中心坐标为(
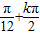 ,0)(k∈Z)
,0)(k∈Z)∵f(x)的图象按
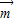 的长度最短的平移
的长度最短的平移∴
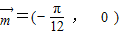 (13分)
(13分)点评:本题考查的知识点是平面向量的数量积运算,正弦型函数的周期,单调性,最值及函数图象的平移变换,是三角函数图象和性质与平面向量的综合应用,熟练掌握正弦型函数的图象和性质是解答本题的关键.

练习册系列答案
相关题目
已知向量
=(sinx,cosx),向量
=(1,
),则|
+
|的最大值为( )
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |