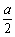题目内容
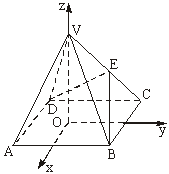
20.(甲)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,
Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(Ⅰ)求cos〈![]() 〉;
〉;
(Ⅱ)记面BCV为![]() ,面DCV为
,面DCV为![]() ,若∠BED是二面角
,若∠BED是二面角![]() -VC-
-VC-![]() 的平面角,求cosBED的值.
的平面角,求cosBED的值.
20.(甲)本小题考查空间直角坐标的概念,空间点和向量的坐标表示以及两个向量夹角的计算方法;考查运用向量研究空间图形的数学思想方法.
解:(Ⅰ)由题意知B(a,a,0),C(-a,a,0),D(―a,―a,0),E(-![]() ),
),
由此得 ![]() =(
=(![]() ),
),![]() =(
=(![]() ).
).
∴ 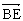 ·
·![]() =(
=(![]() ·
·![]() )+(
)+(![]() ·
·![]() )+
)+![]() ·
·![]() =
=![]() ,
,
|![]() | = |
| = |![]() | =
| =![]() =
=![]()
由向量的数量积公式有
cos〈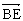 ,
,![]() 〉=
〉=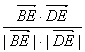
=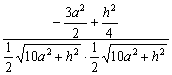
=![]()
(Ⅱ)若∠BED是二面角![]() -VC-
-VC-![]() 的平面角,则,即有
的平面角,则,即有![]()
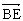 ·
·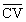 = 0.
= 0.
又C(-a,a,0),V(0,0,h),那么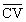 =(a,-a,h),且
=(a,-a,h),且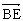 =(
=(![]() ),
),
∴ 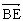 ·
·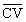 =
=![]() = 0.
= 0.
即h = ![]() a,这时有cos〈
a,这时有cos〈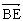 ,
,![]() 〉=
〉=![]() =
=![]() =
=![]() .
.
即cosBED =![]() .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
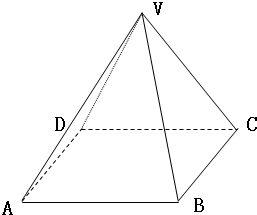 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.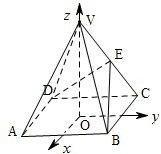 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.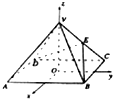 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.