题目内容
[番茄花园1] 本题共有2个小题,第一个小题满分5分,第2个小题满分8分。
已知数列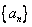 的前
的前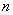 项和为
项和为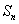 ,且
,且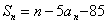 ,
,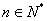
(1)证明: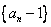 是等比数列;
是等比数列;
(2)求数列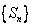 的通项公式,并求出n为何值时,
的通项公式,并求出n为何值时,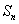 取得最小值,并说明理由。
取得最小值,并说明理由。
同理可得,当n≤15时,数列{Sn}单调递减;故当n=15时,Sn取得最小值.
[番茄花园1]20.
 备战中考寒假系列答案
备战中考寒假系列答案[番茄花园1] (本题满分l4分)如图,一个小球从M处投入,通过管道自
 上而下落A或B或C。已知小球从每个叉口落入左右两个
上而下落A或B或C。已知小球从每个叉口落入左右两个
管道的可能性是相等的.
某商家按上述投球方式进行促销活动,若投入的小球落
到A,B,C,则分别设为l,2,3等奖.
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,
90%.记随变量 为获得k(k=1,2,3)等奖的折扣
为获得k(k=1,2,3)等奖的折扣
率,求随机变量 的分布列及期望
的分布列及期望 ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机
 变量
变量 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求 .
.
[番茄花园1]1.
[番茄花园1] 本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分10分。
若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 远离
远离 .
.
(1)若 比1远离0,求
比1远离0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: 比
比 远离
远离 ;
;
(3)已知函数 的定义域
的定义域 .任取
.任取 ,
, 等于
等于 和
和 中远离0的那个值.写出函数
中远离0的那个值.写出函数 的解析式,并指出它的基本性质(结论不要求证明).
的解析式,并指出它的基本性质(结论不要求证明).
23本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知椭圆 的方程为
的方程为 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足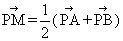 ,求点
,求点 的坐标;
的坐标;
(2)设直线 交椭圆
交椭圆 于
于 、
、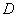 两点,交直线
两点,交直线 于点
于点 .若
.若 ,证明:
,证明: 为
为 的中点;
的中点;
(3)对于椭圆 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆 上存在不同的两个交点
上存在不同的两个交点 、
、 满足
满足 ,写出求作点
,写出求作点 、
、 的步骤,并求出使
的步骤,并求出使 、
、 存在的θ的取值范围.
存在的θ的取值范围.
[番茄花园1]22.
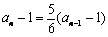 ,
,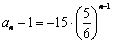 ,得
,得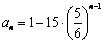 ,从而
,从而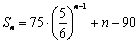 (nÎN*);
(nÎN*);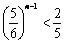 ,
,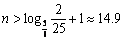 ,当n≥15时,数列{Sn}单调递增;
,当n≥15时,数列{Sn}单调递增;
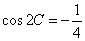
 (1)当圆柱底面半径
(1)当圆柱底面半径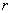 取何值时,
取何值时,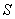 取得最大值?并求出该
取得最大值?并求出该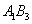 与
与 所在异面直线所成角的大小(结果用反三角函数表示)
所在异面直线所成角的大小(结果用反三角函数表示)