题目内容
空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.①若AC=BD,则四边形EFGH是
②若AC⊥BD,则四边形EFGH是
分析:①结合图形,由三角形的中位线定理可得EF∥AC,GH∥AC且EF=
AC,GH=
AC,由平行四边形的定义可得四边形EFGH是平行四边形,再由邻边相等地,得到四边形EFGH是菱形.
②由①知四边形EFGH是平行四边形,再由邻边垂直得到四边形EFGH是矩形.
| 1 |
| 2 |
| 1 |
| 2 |
②由①知四边形EFGH是平行四边形,再由邻边垂直得到四边形EFGH是矩形.
解答: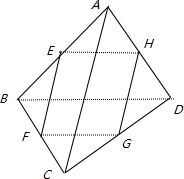 解:如图所示:①∵EF∥AC,GH∥AC且EF=
解:如图所示:①∵EF∥AC,GH∥AC且EF=
AC,GH=
AC
∴四边形EFGH是平行四边形
又∵AC=BD
∴EF=FG
∴四边形EFGH是菱形.
②由①知四边形EFGH是平行四边形
又∵AC⊥BD,
∴EF⊥FG
∴四边形EFGH是矩形.
故答案为:菱形,矩形
 解:如图所示:①∵EF∥AC,GH∥AC且EF=
解:如图所示:①∵EF∥AC,GH∥AC且EF=| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH是平行四边形
又∵AC=BD
∴EF=FG
∴四边形EFGH是菱形.
②由①知四边形EFGH是平行四边形
又∵AC⊥BD,
∴EF⊥FG
∴四边形EFGH是矩形.
故答案为:菱形,矩形
点评:本题主要考查棱锥的结构特征,主要涉及了线段的中点,中位线定理,构成平面图形,研究平面图形的形状,是常考类型,属基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且
如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且