题目内容
由于近几年民用车辆增长过快,造成交通拥堵现象日益严重,现有A、B、C三辆车从同一地点同时出发,开往甲、乙、丙三地,已知A、B、C这三辆车被驶往目的地的过程中,出现堵车的概率依次为 、
、 、
、 ,且每辆车是否被堵互不影响.
,且每辆车是否被堵互不影响.(Ⅰ)求这三辆车恰有一辆车被堵的概率;
(Ⅱ)用ξ表示这三辆车中被堵的车辆数,求ξ的分布列及数学期望Eξ.
【答案】分析:(Ⅰ)这三辆车恰有一辆车被堵,可分为三个互斥事件的概率的和;
(Ⅱ)用ξ表示这三辆车中被堵的车辆数,则ξ可取0,1,2,3,求出相应的概率,即可求得ξ的分布列及数学期望Eξ.
解答:解:(Ⅰ)这三辆车恰有一辆车被堵的概率为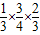 +
+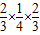 +
+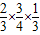 =
= ;
;
(Ⅱ)用ξ表示这三辆车中被堵的车辆数,则ξ可取0,1,2,3
P(ξ=0)=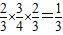 ;P(ξ=1)=
;P(ξ=1)= ,P(ξ=3)=
,P(ξ=3)=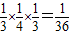 ,
,
P(ξ=2)=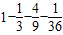 =
=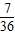
∴ξ的分布列为
数学期望Eξ=0× +1×
+1× +2×
+2×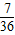 +3×
+3×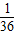 =
=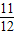 .
.
点评:本题考查互斥事件的概率,考查离散型随机变量的分布列与数学期望,解题的关键是确定变量的取值与含义.
(Ⅱ)用ξ表示这三辆车中被堵的车辆数,则ξ可取0,1,2,3,求出相应的概率,即可求得ξ的分布列及数学期望Eξ.
解答:解:(Ⅰ)这三辆车恰有一辆车被堵的概率为
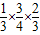 +
+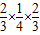 +
+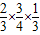 =
= ;
;(Ⅱ)用ξ表示这三辆车中被堵的车辆数,则ξ可取0,1,2,3
P(ξ=0)=
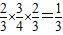 ;P(ξ=1)=
;P(ξ=1)= ,P(ξ=3)=
,P(ξ=3)=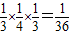 ,
,P(ξ=2)=
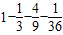 =
=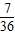
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |  |  | 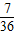 | 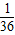 |
 +1×
+1× +2×
+2×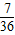 +3×
+3×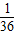 =
=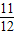 .
.点评:本题考查互斥事件的概率,考查离散型随机变量的分布列与数学期望,解题的关键是确定变量的取值与含义.

练习册系列答案
相关题目
 、
、 、
、 、
、 、
、 ,且每辆车是否被堵互不影响.
,且每辆车是否被堵互不影响. 表示这三辆车中被堵的车辆数,求
表示这三辆车中被堵的车辆数,求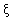 的分布列及数学期望E
的分布列及数学期望E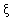 .
.