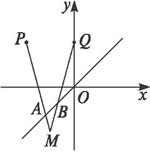
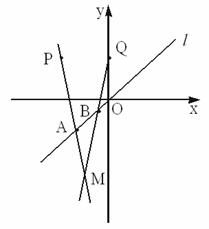
题目内容
 已知两点P(-2,2),Q(0,2)以及一条直线:L:y=x,设长为
已知两点P(-2,2),Q(0,2)以及一条直线:L:y=x,设长为| 2 |
分析:根据题意,设点A和B分别是(a,a)和(a+1,a+1),直线PA的方程是y-2=
(x+2)(a≠-2)(1),直线QB的方程是y-2=
x(a≠-1)(2).当
=
,即a=0时,直线PA和QB平行,无交点;当a≠0时,直线PA与QB相交,
设交点为M(x,y),y-2=(1-
)x,a+1=
,∴a+2=
,a-2=
.由此能得到直线PA和QB的交点M的轨迹方程.
| a-2 |
| a+2 |
| a-1 |
| a+1 |
| a-2 |
| a+2 |
| a-1 |
| a+1 |
设交点为M(x,y),y-2=(1-
| 2 |
| a+1 |
| 2x |
| x-y+2 |
| 3x-y+2 |
| x-y+2 |
| 3y-x-6 |
| x-y+2 |
解答:解:由于线段AB在直线y=x上移动,且AB的长
,
所以可设点A和B分别是(a,a)和(a+1,a+1),其中a为参数
于是可得:直线PA的方程是y-2=
(x+2)(a≠-2)(1)
直线QB的方程是y-2=
x(a≠-1)(2)
(1)当
=
,即a=0时,
直线PA和QB平行,无交点
(2)当a≠0时,直线PA与QB相交,
设交点为M(x,y),由(2)式得y-2=(1-
)x,a+1=
,
∴a+2=
,a-2=
.
将上述两式代入(1)式,得
y-2=
(x+2)整理得x2-y2+2x-2y+8=0,
即
-
=-1(*)
当a=-2或a=-1时,直线PA和QB仍然相交,并且交点坐标也满足(*)式
所以(*)式即为所求动点的轨迹方程.
| 2 |
所以可设点A和B分别是(a,a)和(a+1,a+1),其中a为参数
于是可得:直线PA的方程是y-2=
| a-2 |
| a+2 |
直线QB的方程是y-2=
| a-1 |
| a+1 |
(1)当
| a-2 |
| a+2 |
| a-1 |
| a+1 |
直线PA和QB平行,无交点
(2)当a≠0时,直线PA与QB相交,
设交点为M(x,y),由(2)式得y-2=(1-
| 2 |
| a+1 |
| 2x |
| x-y+2 |
∴a+2=
| 3x-y+2 |
| x-y+2 |
| 3y-x-6 |
| x-y+2 |
将上述两式代入(1)式,得
y-2=
| 3y-x-6 |
| 3x-y+2 |
即
| (x+1)2 |
| 8 |
| (y+1)2 |
| 8 |
当a=-2或a=-1时,直线PA和QB仍然相交,并且交点坐标也满足(*)式
所以(*)式即为所求动点的轨迹方程.
点评:本题考查轨迹方程的求法,解题时要认真审题,仔细分析,注意挖掘题设中的隐含条件,合理地选取公式.

练习册系列答案
相关题目