Question

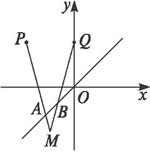
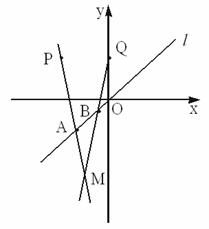
已知两点P（-2，2），Q（0，2）以及一条直线：L:y=x，设长为的线段AB在直线L上移动，如图。求直线PA和QB的交点M的轨迹方程。（要求把结果写成普通方程）

      

 

                       

Answer 1

解：由于线段AB在直线y=x上移动，且AB的长，所以可设点A和B分别是（,)和(+1,+1)，其中为参数。

于是可得：直线PA的方程是

直线QB的方程是

1.当直线PA和QB平行，无交点。

2．当时，直线PA与QB相交，设交点为M(x,y)，由（2）式得

将上述两式代入（1）式，得

当=-2或=-1时，直线PA和QB仍然相交，并且交点坐标也满足（*）式。

所以（*）式即为所求动点的轨迹方程。