题目内容
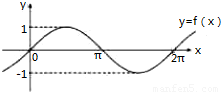函数y=f（x）的图象如图所示，若
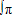f（x）dx=m，则
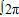f（x）dx等于（ ）A．m
B．2m
C．0
D．-m
【答案】分析：根据定积分的几何意义知，定积分的值∫2πf（x）dx是f（x）的图象与x轴所围成的平面图形的面积的代数和，结合函数y=f（x）的图象的对称性即可解决问题．
解答：
解：原式=∫πf（x）dx+∫π2πf（x）dx．
∵原函数y=f（x）的图象如图所示，
∴在x轴两侧的图象关于点（π，0）对称，
∴对应的面积大小相等，其代数和为：0．
则∫2πf（x）dx等于0．
故选C．
点评：本题主要考查定积分以及定积分的几何意义，属于基础题．
解答：
解：原式=∫πf（x）dx+∫π2πf（x）dx．∵原函数y=f（x）的图象如图所示，
∴在x轴两侧的图象关于点（π，0）对称，
∴对应的面积大小相等，其代数和为：0．
则∫2πf（x）dx等于0．
故选C．
点评：本题主要考查定积分以及定积分的几何意义，属于基础题．
练习册系列答案
相关题目
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示，给出关于f（x）的下列命题：