题目内容
把函数y=lnx-2的图象按向量
=(-1,2)平移得到函数y=f(x)的图象.
(1)若x>0,证明;f(x)>
;
(2不等式
x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.
| α |
(1)若x>0,证明;f(x)>
| 2x |
| x+2 |
(2不等式
| 1 |
| 2 |
分析:(1)先根据向量的平移,求得f(x)=ln(x+1),再构建函数F(x)=f(x)-
=ln(x+1)-
,确定函数的单调性,从而可证不等式;
(2)不等式
x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,等价于
-ln(x2+1)≤m2-2bm-3,对b∈[-1,1],x∈[-1,1]时恒成立,求出左边函数的最大值,进一步可化为对b∈[-1,1]时,0≤m2-2bm-3恒成立,即使2mb+3-m2≤0恒成立,从而可求实数m的取值范围.
| 2x |
| x+2 |
| 2x |
| x+2 |
(2)不等式
| 1 |
| 2 |
| x2 |
| 2 |
解答:(1)证明:∵函数y=lnx-2的图象按向量
=(-1,2)平移得到函数y=f(x)的图象
∴f(x)=ln(x+1),
构建函数F(x)=f(x)-
=ln(x+1)-
,
求导函数得F′(x)=
-
=
=
∵x>0,∴F′(x)>0,
∴在(0,+∞)上,F(x)为增函数.
∴F(x)>F(0)=0,
∴f(x)-
>0
∴f(x)>
;
(2)解:∵不等式
x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立
∴
-ln(x2+1)≤m2-2bm-3,对b∈[-1,1],x∈[-1,1]时恒成立
设g(x)=
-ln(x2+1),
则g′(x)=x-
=
=
,
x∈(-1,0)时,g′(x)>0,x∈(0,1)时,g′(x)<0.
∴x∈(-1,1)时,g(x)≤g(0)=0.
∴x∈(-1,1)时,0≤m2-2bm-3,
∴问题可化为对b∈[-1,1]时,0≤m2-2bm-3恒成立,即使2mb+3-m2≤0恒成立.
∴
或
,
∴m≤-3或m≥3
综上,实数m的取值范围是(-∞,-3]∪[3,+∞).
| α |
∴f(x)=ln(x+1),
构建函数F(x)=f(x)-
| 2x |
| x+2 |
| 2x |
| x+2 |
求导函数得F′(x)=
| 1 |
| x+1 |
| 4 |
| (x+2)2 |
| (x+2)2-4(x+1) |
| (x+1)(x+2)2 |
| x2 |
| (x+1)(x+2)2 |
∵x>0,∴F′(x)>0,
∴在(0,+∞)上,F(x)为增函数.
∴F(x)>F(0)=0,
∴f(x)-
| 2x |
| x+2 |
∴f(x)>
| 2x |
| x+2 |
(2)解:∵不等式
| 1 |
| 2 |
∴
| x2 |
| 2 |
设g(x)=
| x2 |
| 2 |
则g′(x)=x-
| 2x |
| x2+1 |
| x3-x |
| x2+1 |
| x(x+1)(x-1) |
| x2+1 |
x∈(-1,0)时,g′(x)>0,x∈(0,1)时,g′(x)<0.
∴x∈(-1,1)时,g(x)≤g(0)=0.
∴x∈(-1,1)时,0≤m2-2bm-3,
∴问题可化为对b∈[-1,1]时,0≤m2-2bm-3恒成立,即使2mb+3-m2≤0恒成立.
∴
|
|
∴m≤-3或m≥3
综上,实数m的取值范围是(-∞,-3]∪[3,+∞).
点评:本题重点考查导数知识的运用,考查利用导数确定函数的单调性,进而证明不等式,考查恒成立问题的理解与处理,综合性强.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
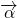 =(-1,2)平移得到函数y=f(x)的图象.
=(-1,2)平移得到函数y=f(x)的图象. ;
; x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.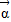 =(-1,2)平移得到函数y=f(x)的图象.
=(-1,2)平移得到函数y=f(x)的图象. ;
; x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.