题目内容
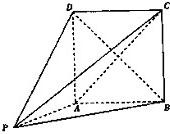如图，在几何体P-ABCD中，四边形ABCD为矩形，PA⊥平面ABCD，AB=PA=2．（1）当AD=2时，求证：平面PBD⊥平面PAC；
（2）若PC与AD所成角为45°，求几何体P-ABCD的体积．
分析：（1）要证平面PBD⊥平面PAC，只需证明平面ABCD内的直线BD，垂直平面PBD必定两条相交直线PA、AC即可；
（2）PC与AD所成角为45°，证明BC⊥平面PAB，求出底面ABCD的面积和高，求几何体P-ABCD的体积．
（2）PC与AD所成角为45°，证明BC⊥平面PAB，求出底面ABCD的面积和高，求几何体P-ABCD的体积．
解答：解：（1）当AD=2时，四边形ABCD是正方形，则BD⊥AC，（2分）
∵PA⊥平面ABCD，BD?平面ABCD，∴PA⊥BD，（4分）
又PA∩AC=A，∴BD⊥平面PAC，∵BD?平面PBD
∴平面PBD⊥平面PAC；（6分）
（2）若PC与AD成45°角，AD∥BC，则∠PCB=45°．（8分）
∵BC⊥AB，BC⊥PA，AB∩PA=A
∴BC⊥平面PAB，PB?平面PAB
∴BC⊥PB（10分）
∴∠CPB=90°-45°=45°，∴BC=PB=2
∴几何体P-ABCD的体积为
×(2×2
)×2=
．（12分）
∵PA⊥平面ABCD，BD?平面ABCD，∴PA⊥BD，（4分）
又PA∩AC=A，∴BD⊥平面PAC，∵BD?平面PBD
∴平面PBD⊥平面PAC；（6分）
（2）若PC与AD成45°角，AD∥BC，则∠PCB=45°．（8分）
∵BC⊥AB，BC⊥PA，AB∩PA=A
∴BC⊥平面PAB，PB?平面PAB
∴BC⊥PB（10分）
∴∠CPB=90°-45°=45°，∴BC=PB=2
| 2 |
∴几何体P-ABCD的体积为
| 1 |
| 3 |
| 2 |
8
| ||
| 3 |
点评：本题考查平面与平面垂直的判定，棱锥的体积，考查空间想象能力，逻辑思维能力，是中档题．
练习册系列答案
相关题目
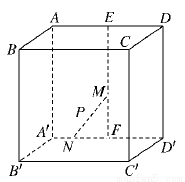
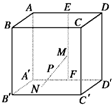如图，在棱长为4的正方体ABCD-A′B′C′D′中，E、F分别是AD、A′D′的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A′B′C′D′上运动，则线段MN的中点P的轨迹（曲面）与二面角A-A′D′-B′所围成的几何体的体积为（ ）
（1）已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′如图所示，其中A′D′=2，B′C′=4，A′B′=1，求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积．
如图，在边长为12的正方形A1 AA′A1′中，点B、C在线段AA′上，且AB = 3，BC = 4，作BB1∥AA1，分别交A1A1′、AA1′于点B1、P；作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q；将该正方形沿BB1、CC1折叠，使得A′A1′ 与AA1重合，构成如图所示的三棱柱ABC—A1B1C1，在三棱柱ABC—A1B1C1中， （Ⅰ）求证：AB⊥平面BCC1B1； （Ⅱ）求面PQA与面ABC所成的锐二面角的大小．（Ⅲ）求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比．
