题目内容
(本小题12分)已知二次函数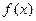 满足
满足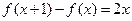 且
且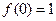 .
.
(1)求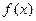 的解析式;
的解析式;
(2) 当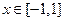 时,不等式:
时,不等式: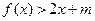 恒成立,求实数
恒成立,求实数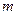 的范围.
的范围.
(3)设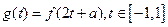
 ,求
,求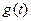 的最大值;
的最大值;
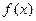 满足
满足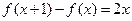 且
且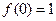 .
.(1)求
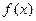 的解析式;
的解析式;(2) 当
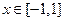 时,不等式:
时,不等式: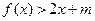 恒成立,求实数
恒成立,求实数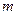 的范围.
的范围.(3)设
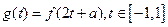
 ,求
,求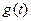 的最大值;
的最大值; (1)
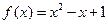
(2)

(3)
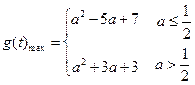
(1)解:令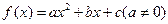 代入:
代入:

得:
∴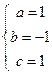 ∴
∴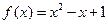
(2)当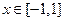 时,
时,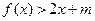 恒成立
恒成立
即: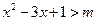 恒成立;
恒成立;
令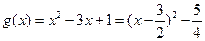 ,
,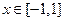
则对称轴: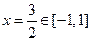 ,
,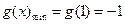
∴
(3)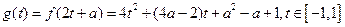
对称轴为: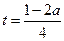
当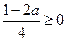 时,即:
时,即: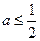 ;如图1:
;如图1:

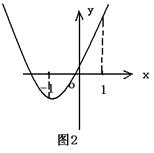
②当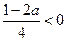 时,即:
时,即: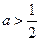 ;如图2:
;如图2:
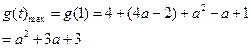
综上所述: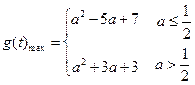
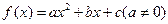 代入:
代入:

得:

∴
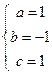 ∴
∴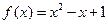
(2)当
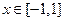 时,
时,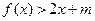 恒成立
恒成立即:
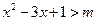 恒成立;
恒成立;
令
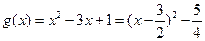 ,
,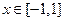
则对称轴:
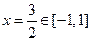 ,
,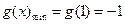
∴

(3)
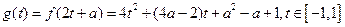
对称轴为:
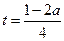
当
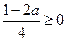 时,即:
时,即: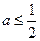 ;如图1:
;如图1:
②当
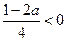 时,即:
时,即: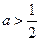 ;如图2:
;如图2: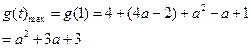
综上所述:
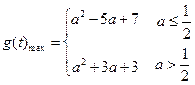

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 是圆
是圆 上的动点,定点
上的动点,定点 ,则
,则








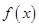 =
=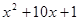 ,则函数
,则函数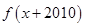 的最小值及对称轴方程分别为( )
的最小值及对称轴方程分别为( ) 函数
函数 .
.
 的图象在点
的图象在点 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为 ,
, ,数列
,数列 的通项公式为 .
的通项公式为 .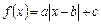 满足①函数
满足①函数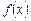 的图象关于
的图象关于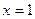 对称;②在
对称;②在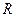 上有大于零的最大值;③函数
上有大于零的最大值;③函数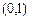 ;④
;④ ,试写出一组符合要
,试写出一组符合要 求的
求的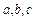 的值
的值  1);(2)g(x)
1);(2)g(x) ,则a="( " )
,则a="( " )


 在
在 上具有单调性,那么实数
上具有单调性,那么实数 的取值范围是 .
的取值范围是 .