题目内容
已知矩阵A=
,列向量X=
,Y=
(1)用逆矩阵方法解方程(组)AX=Y;
(2)用特征向量与特征值求A11×
的值.
|
|
|
(1)用逆矩阵方法解方程(组)AX=Y;
(2)用特征向量与特征值求A11×
|
(1)系数行列式△=|A|=-56-(-54)=-2,矩阵A可逆.
逆矩阵为A-1=-
=
…(3分)
由
=
,得
=
=
…(5分)
∴原方程组的解是
…(6分)
(2)特征矩阵为
,特征多项式为(7-λ)(-8-λ)-54,即λ2+λ-2…(8分)
解方程λ2+λ-2=0,求得特征值λ1=1,λ2=-2…(9分)
当λ=1时,对应的特征向量为X1=
当λ=-2时,对应的特征向量为X2=
,…(10分)
设
=m
+n
,解此方程组得m=-20,n=-1…(11分)
∴A11×
=(-20)×111×
+(-1)×(-2)11
=
=
.
逆矩阵为A-1=-
| 1 |
| 2 |
|
|
由
|
|
|
|
|
|
|
∴原方程组的解是
|
(2)特征矩阵为
|
解方程λ2+λ-2=0,求得特征值λ1=1,λ2=-2…(9分)
当λ=1时,对应的特征向量为X1=
|
当λ=-2时,对应的特征向量为X2=
|
设
|
|
|
∴A11×
|
|
|
|
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 1=4及对应的一个特征向量e1=
1=4及对应的一个特征向量e1=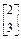 ,并有特征值
,并有特征值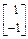 .
. ,且
,且 ,则
,则 =
=