题目内容
已知F1、F2为双曲线 的左、右焦点,P为右支上任意一点,若
的左、右焦点,P为右支上任意一点,若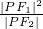 的最小值为8a,则该双曲线的离心率e的取值范围为
的最小值为8a,则该双曲线的离心率e的取值范围为
- A.(1,2]
- B.(1,3]
- C.[2,3]
- D.[3,+∞)
B
分析:由定义知:|PF1|-|PF2|=2a,|PF1|=2a+|PF2|,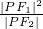 =
=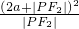 =
=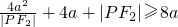 ,当且仅当
,当且仅当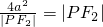 ,即|PF2|=2a时取得等号.再由焦半径公式得双曲线的离心率e>1的取值范围.
,即|PF2|=2a时取得等号.再由焦半径公式得双曲线的离心率e>1的取值范围.
解答:由定义知:|PF1|-|PF2|=2a,
|PF1|=2a+|PF2|
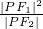 =
=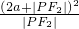
=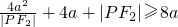 ,
,
当且仅当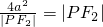 ,
,
即|PF2|=2a时取得等号
设P(x0,y0) (x0≤-a)
由焦半径公式得:
|PF2|=-ex0-a=2a
ex0=-2a
e=-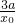 ≤3
≤3
又双曲线的离心率e>1
∴e∈(1,3]
故选B.
点评:本题考查双曲线的性质和应用,解题时要认真审题,注意焦半径公式的合理运用.
分析:由定义知:|PF1|-|PF2|=2a,|PF1|=2a+|PF2|,
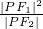 =
=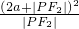 =
=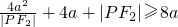 ,当且仅当
,当且仅当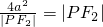 ,即|PF2|=2a时取得等号.再由焦半径公式得双曲线的离心率e>1的取值范围.
,即|PF2|=2a时取得等号.再由焦半径公式得双曲线的离心率e>1的取值范围.解答:由定义知:|PF1|-|PF2|=2a,
|PF1|=2a+|PF2|
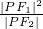 =
=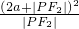
=
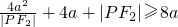 ,
,当且仅当
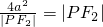 ,
,即|PF2|=2a时取得等号
设P(x0,y0) (x0≤-a)
由焦半径公式得:
|PF2|=-ex0-a=2a
ex0=-2a
e=-
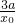 ≤3
≤3又双曲线的离心率e>1
∴e∈(1,3]
故选B.
点评:本题考查双曲线的性质和应用,解题时要认真审题,注意焦半径公式的合理运用.

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )