题目内容
已知数列:2,0,2,0,2,0,….前六项不适合下列哪个通项公式( )A.an=1+(-1)n+1
B.an=2|sin
 |
|C.an=1-(-1)n
D.an=2sin

【答案】分析:对四个选项中的通项公式的n分别取前六项,看其是否是数列2,0,2,0,2,0,从而得到结论.
解答:解:对于选项A,an=1+(-1)n+1取前六项得2,0,2,0,2,0满足条件;
对于选项B,an=2|sin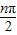 |取前六项得2,0,2,0,2,0满足条件;
|取前六项得2,0,2,0,2,0满足条件;
对于选项C,an=1-(-1)n取前六项得2,0,2,0,2,0满足条件;
对于选项D,an=2sin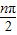 取前六项得2,0,-2,0,2,0不满足条件;
取前六项得2,0,-2,0,2,0不满足条件;
故选D
点评:本题主要考查了数列的概念及其简单表示,同时考查了列举法进行验证,属于基础题.
解答:解:对于选项A,an=1+(-1)n+1取前六项得2,0,2,0,2,0满足条件;
对于选项B,an=2|sin
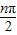 |取前六项得2,0,2,0,2,0满足条件;
|取前六项得2,0,2,0,2,0满足条件;对于选项C,an=1-(-1)n取前六项得2,0,2,0,2,0满足条件;
对于选项D,an=2sin
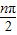 取前六项得2,0,-2,0,2,0不满足条件;
取前六项得2,0,-2,0,2,0不满足条件;故选D
点评:本题主要考查了数列的概念及其简单表示,同时考查了列举法进行验证,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列:2,0,2,0,2,0,….前六项不适合下列哪个通项公式( )
| A、an=1+(-1)n+1 | ||
B、an=2|sin
| ||
| C、an=1-(-1)n | ||
D、an=2sin
|
 |
| |
|