题目内容
已知直线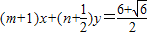 与圆
与圆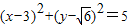 相切,若对任意的m,n∈R+均有不等式2m+n≥k成立,那么正整数k的最大值是( )
相切,若对任意的m,n∈R+均有不等式2m+n≥k成立,那么正整数k的最大值是( )A.3
B.5
C.7
D.9
【答案】分析:利用圆心(3,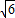 )到直线(m+1)x+(n+
)到直线(m+1)x+(n+ )y-
)y-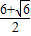 =0的距离等于半径
=0的距离等于半径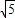 ,令2m+n=t,求得t的最小值即为正整数k的最大值.
,令2m+n=t,求得t的最小值即为正整数k的最大值.
解答:解:∵直线(m+1)x+(n+ )y-
)y-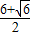 =0与圆(x-3)2+
=0与圆(x-3)2+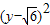 =5相切,
=5相切,
∴圆心(3,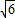 )到直线(m+1)x+(n+
)到直线(m+1)x+(n+ )y-
)y-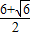 =0的距离d等于半径
=0的距离d等于半径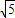 ,
,
即d=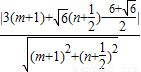 =
=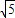 ,
,
∴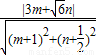 =
=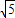 ,
,
两端平方,整理得:4m2+n2-5(2m+n)-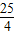 =-6
=-6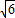 mn,
mn,
即(2m+n)2-5(2m+n)-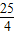 =(4-6
=(4-6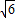 )mn.
)mn.
∴(3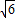 -2)•2mn=
-2)•2mn=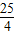 +5(2m+n)-(2m+n)2≤(3
+5(2m+n)-(2m+n)2≤(3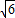 -2)•
-2)•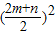 ,
,
令t=2m+n(t>0),
则(3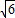 +2)t2-20t-25≥0,
+2)t2-20t-25≥0,
∵△=(-20)2-4×(-25)×(3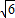 +2)=600+300
+2)=600+300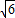 ,
,
∴t≥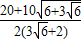 =
=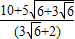 ,
,
∴tmin=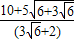 ∈(3,4),
∈(3,4),
∵正整数k≤2m+n=t恒成立,
∴k=3.
故选A.
点评:本题考查直线与圆的位置关系,突出考查点到直线间的距离及运算能力,考查转化思想与方程思想的综合应用,属于难题.
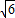 )到直线(m+1)x+(n+
)到直线(m+1)x+(n+ )y-
)y-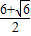 =0的距离等于半径
=0的距离等于半径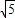 ,令2m+n=t,求得t的最小值即为正整数k的最大值.
,令2m+n=t,求得t的最小值即为正整数k的最大值.解答:解:∵直线(m+1)x+(n+
 )y-
)y-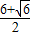 =0与圆(x-3)2+
=0与圆(x-3)2+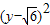 =5相切,
=5相切,∴圆心(3,
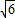 )到直线(m+1)x+(n+
)到直线(m+1)x+(n+ )y-
)y-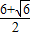 =0的距离d等于半径
=0的距离d等于半径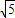 ,
,即d=
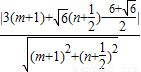 =
=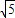 ,
,∴
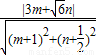 =
=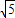 ,
,两端平方,整理得:4m2+n2-5(2m+n)-
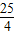 =-6
=-6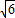 mn,
mn,即(2m+n)2-5(2m+n)-
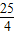 =(4-6
=(4-6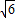 )mn.
)mn.∴(3
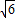 -2)•2mn=
-2)•2mn=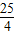 +5(2m+n)-(2m+n)2≤(3
+5(2m+n)-(2m+n)2≤(3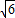 -2)•
-2)•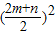 ,
,令t=2m+n(t>0),
则(3
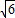 +2)t2-20t-25≥0,
+2)t2-20t-25≥0,∵△=(-20)2-4×(-25)×(3
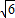 +2)=600+300
+2)=600+300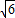 ,
,∴t≥
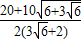 =
=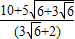 ,
,∴tmin=
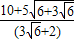 ∈(3,4),
∈(3,4),∵正整数k≤2m+n=t恒成立,
∴k=3.
故选A.
点评:本题考查直线与圆的位置关系,突出考查点到直线间的距离及运算能力,考查转化思想与方程思想的综合应用,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
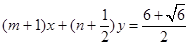 与圆
与圆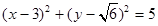 相切,若对任意的
相切,若对任意的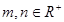 均有不等式
均有不等式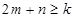 成立,那么正整数
成立,那么正整数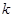 的最大值是( )
的最大值是( )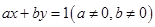 与圆
与圆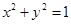 相切,若
相切,若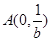 ,
,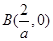 ,则
,则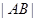 的最小值为 .
的最小值为 .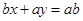 与圆
与圆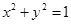 相切,若
相切,若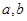 同号,则
同号,则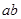 的最小值为( )
的最小值为( )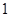 B.
B.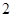 C.
C.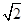 D.不存在
D.不存在