题目内容
已知直线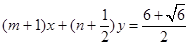 与圆
与圆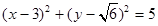 相切,若对任意的
相切,若对任意的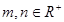 均有不等式
均有不等式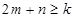 成立,那么正整数
成立,那么正整数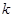 的最大值是( )
的最大值是( )
A.3 B.5 C.7 D.9
【答案】
A
【解析】
试题分析:∵直线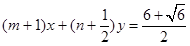 与圆
与圆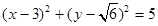 相切,∴
相切,∴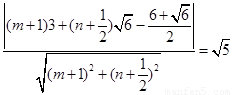 ,即
,即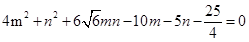 (※),令t=2m+n,则n=t-2m,代入(※)化简得
(※),令t=2m+n,则n=t-2m,代入(※)化简得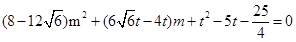 ,由题意该式有解,∴其判别式
,由题意该式有解,∴其判别式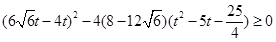 ,解得t≥3,故正整数
,解得t≥3,故正整数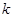 的最大值是3,故选A
的最大值是3,故选A
考点:本题考查了直线与圆的位置关系
点评:研究直线和圆的位置关系的相关问题时通常采用“几何法”即抓住圆心到直线的的距离与半径的关系

练习册系列答案
相关题目
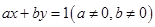 与圆
与圆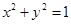 相切,若
相切,若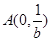 ,
,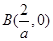 ,则
,则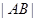 的最小值为 .
的最小值为 .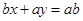 与圆
与圆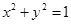 相切,若
相切,若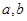 同号,则
同号,则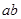 的最小值为( )
的最小值为( )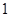 B.
B.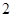 C.
C.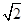 D.不存在
D.不存在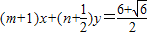 与圆
与圆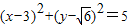 相切,若对任意的m,n∈R+均有不等式2m+n≥k成立,那么正整数k的最大值是( )
相切,若对任意的m,n∈R+均有不等式2m+n≥k成立,那么正整数k的最大值是( )