题目内容
20.抛物线E:y2=2px(p>0)的焦点为F,过F且斜率为l的直线,交E于A,B两点,线段AB的中点M的纵坐标为2.(1)求点M到E的准线的距离;
(2)设E的准线与x轴的交点为P,将直线l绕点F旋转直某一位置得直线l′,l′交E与C,D两点,E上是否存在一点N,满足$\overrightarrow{PC}$$+\overrightarrow{PD}$=$\overrightarrow{PN}$?若存在,求直线l′的斜率;若不存在,请说明理由.
分析 (1)先假设A,B的坐标,根据A,B满足抛物线方程,将其代入得到两个关系式,再将两个关系式相减,根据直线的斜率和线段AB的中点的纵坐标的值可求出p的值,进而得到焦点和准线方程,由斜率公式可得M的横坐标,即可得到所求距离;
(2)设出直线l'的方程,代入抛物线方程,运用韦达定理,E上假设存在一点N,满足$\overrightarrow{PC}$$+\overrightarrow{PD}$=$\overrightarrow{PN}$,设N($\frac{{n}^{2}}{4}$,n),由向量的坐标运算,即可判断是否存在.
解答 解:(1)设A(x1,y1)、B(x2,y2),
则有y12=2px1,y22=2px2,
两式相减得:(y1-y2)(y1+y2)=2p(x1-x2),
又因为直线的斜率为1,所以$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=1,
所以有y1+y2=2p,又线段AB的中点的纵坐标为2,
即y1+y2=4,所以p=2,
所以抛物线y2=4x的焦点F(1,0),准线方程为x=-1.
MF的斜率为1,可得M的横坐标为3,
即有M(3,2)到准线的距离为3+1=4;
(2)由抛物线的准线方程,可得P(-1,0),
可设直线l':y=k(x-1),
设C(x3,y3)、D(x4,y4),
将直线l'方程代入抛物线方程,可得k2x2-(2k2+4)x+k2=0,
即有x3+x4=2+$\frac{4}{{k}^{2}}$,
y3+y4=k(x3+x4-2)=$\frac{4}{k}$,
E上假设存在一点N,满足$\overrightarrow{PC}$$+\overrightarrow{PD}$=$\overrightarrow{PN}$,
设N($\frac{{n}^{2}}{4}$,n),则x3+x4+2=$\frac{{n}^{2}}{4}$+1,y3+y4=n,
即有n=$\frac{4}{k}$,且3+$\frac{4}{{k}^{2}}$=$\frac{{n}^{2}}{4}$,
即为3+$\frac{{n}^{2}}{4}$=$\frac{{n}^{2}}{4}$,无解.
故E上不存在一点N,满足$\overrightarrow{PC}$$+\overrightarrow{PD}$=$\overrightarrow{PN}$.
点评 本题考查抛物线的几何性质、直线与抛物线的位置关系,向量的坐标运算等基础知识,属于中档题.

| A. | 32014 | B. | 32014-1 | C. | 32015 | D. | 32015-1 |
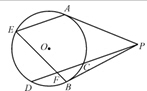 过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.
过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.