Question

在30°的二面角的一个面内有一个点，若它刭另一个面的距离是10，求它到棱的距离．

Answer 1

分析：如图，PO是它到另一个面β的距离，PH它到棱的距离，得出∠PHO为二面角α-l-β的平面角．在RT△PHO中求解即可．

解答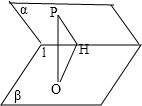：解：如图所示：
P为二面角α-l-β的一个面α内有一点．
PO是它到另一个面β的距离，PO=10．PH它到棱的距离．
∵PO⊥β，∴PO⊥l，又PH⊥l，∴l⊥面POH，得出l⊥OH，
所以∠PHO为二面角α-l-β的平面角，∠PHO=30°．
在RT△PHO中，PH=

PO

sin∠PHO

=

10

1 2

=20

点评：本题考查二面角的定义，空间距离求解．考查空间想象能力，推理论证，运算求解能力．