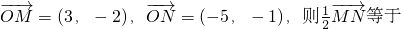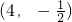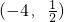题目内容
已知向量
=(8,
x),
=(x,1),x>0,若
-2
与2
+
共线,则x的值为( )
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| a |
| b |
分析:由题意和向量的坐标运算求出
-2
和2
+
的坐标,再代入向量共线的坐标条件列出方程求解.
| a |
| b |
| a |
| b |
解答:解:由题意得,
-2
=(8,
x)-2(x,1)=(8-2x,
x-2),
2
+
=2(8,
x)+(x,1)=(16+x,x+1),
∵
-2
与2
+
共线,
∴(8-2x)(x+1)-(
x-2)(16+x)=0,
解得x2=16,即x=±4,
∵x>0,∴x=4,
故选A.
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
2
| a |
| b |
| 1 |
| 2 |
∵
| a |
| b |
| a |
| b |
∴(8-2x)(x+1)-(
| 1 |
| 2 |
解得x2=16,即x=±4,
∵x>0,∴x=4,
故选A.
点评:本题考查向量共线的坐标表示,属基础题.

练习册系列答案
相关题目
已知向量a=(8,
x,x).b=(x,1,2),其中x>0.若a∥b,则x的值为( )
| 1 |
| 2 |
| A、8 | B、4 | C、2 | D、0 |