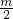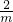题目内容
若tan2α=m,则cotα-tanα=( )A.
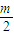
B.
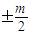
C.

D.
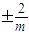
【答案】分析:根据正切函数和余切函数的互为倒数关系,把余切变为正切,通分整理,恰好变为正切的二倍角公式的倒数,整理好系数,得到结果.
解答:解:∵cotα-tanα=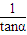 -tanα
-tanα
=
=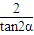
=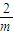
故选C.
点评:利用同角三角函数的基本关系式解决问题:(1)已知某角的一个三角函数值,求该角的其它三角函数值的方法.(2)求值时要注意各三角函数的符号,必要时分类讨论.(3)三角函数式的化简的方法和结果应满足要求.正切的二倍角公式的用法是本题比较灵活的地方,体现公式的正用、逆用、变形用.
解答:解:∵cotα-tanα=
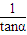 -tanα
-tanα=

=
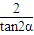
=
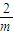
故选C.
点评:利用同角三角函数的基本关系式解决问题:(1)已知某角的一个三角函数值,求该角的其它三角函数值的方法.(2)求值时要注意各三角函数的符号,必要时分类讨论.(3)三角函数式的化简的方法和结果应满足要求.正切的二倍角公式的用法是本题比较灵活的地方,体现公式的正用、逆用、变形用.

练习册系列答案
相关题目
若tan2α=m,则cotα-tanα=( )
A、
| ||
B、±
| ||
C、
| ||
D、±
|
若sinα=m,α为第二象限角,则tan2α的值为( )
A、-
| ||||
B、
| ||||
C、±
| ||||
| D、以上全不对 |