Question

20．已知圆P过点A（1，0），且圆心P（a，2）（a≠0）到直线m：4x-3y+1=0的距离为1，以坐标原点为对称中心且交点落在y轴上的椭圆Ω的离心率与直线2$\sqrt{2}$x-2y+3=0的斜率互为倒数，过点A作一条不与x轴垂直的直线l与椭圆Ω交于C，D两点．
（1）求直线m被圆P所截得的弦长；
（2）若B（4，0），x轴恰为∠CBD的角平分线，求椭圆Ω的标准方程．

Answer 1

分析 （1）由圆心到直线的距离列式求出圆的圆心坐标，再由两点间的距离求出圆的半径，由圆的半径、弦心距和弦长间的关系求得直线m被圆P所截得的弦长；
（2）求直线的斜率，得到椭圆的离心率，进一步得到椭圆长半轴长和短半轴长的关系，得到椭圆方程，设出直线l的方程，和椭圆方程联立，利用根与系数的关系结合x轴恰好为∠CBD的角平分线列式求得b，则椭圆方程可求．

解答 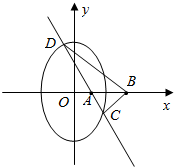解：（1）由题意可知，$\frac{|4a-6+1|}{\sqrt{{4}^{2}+（-3）^{2}}}=1$，解得a=$\frac{5}{2}$，
∴圆心坐标为（$\frac{5}{2}，2$），则半径为$\sqrt{（\frac{5}{2}-1）^{2}+{2}^{2}}=\frac{5}{2}$，
∴圆P的标准方程为$（x-\frac{5}{2}）^{2}+（y-2）^{2}=\frac{25}{4}$，
则直线m被圆P所截得的弦长为$2×\sqrt{\frac{25}{4}-1}=2×\frac{\sqrt{21}}{2}=\sqrt{21}$；
（2）由题意设椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$（a＞b＞0），
∵直线2$\sqrt{2}$x-2y+3=0的斜率为$\sqrt{2}$，∴椭圆的离心率为$\frac{\sqrt{2}}{2}$，
即$\frac{c}{a}=\frac{\sqrt{2}}{2}$，∴$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$，则a²=2b²．
∴椭圆方程为2x²+y²=2b²．
如图，
设过A的直线l的方程为y-0=k（x-1），即y=kx-k．
联立$\left\{\begin{array}{l}{y=kx-x}\\{2{x}^{2}+{y}^{2}=2{b}^{2}}\end{array}\right.$，得（2+k²）x²-2k²x+k²-2b²=0．
设C（x₁，y₁），D（x₂，y₂），
则${x}_{1}+{x}_{2}=\frac{2{k}^{2}}{{k}^{2}+2}$，${x}_{1}{x}_{2}=\frac{{k}^{2}-2{b}^{2}}{{k}^{2}+2}$，
由x轴恰好为∠CBD的角平分线，得$\frac{{y}_{1}}{{x}_{1}-4}=-\frac{{y}_{2}}{{x}_{2}-4}$，即2x₁x₂-5（x₁+x₂）+8=0．
∴$\frac{2{k}^{2}-4{b}^{2}}{{k}^{2}+2}-\frac{10{k}^{2}}{{k}^{2}+2}$+8=0，即b²=4．
∴椭圆Ω方程为：$\frac{{y}^{2}}{8}+\frac{{x}^{2}}{4}=1$．

点评 本题考查了圆的标准方程的求法，考查了直线与椭圆的位置关系，训练了“设而不求”的解题思想方法，是中档题