Question

已知三棱柱ABC-A₁B₁C₁，底面三角形ABC为正三角形，侧棱AA₁⊥底面ABC，AB=2，AA₁=4，E为AA₁的中点，F为BC的中点
（1）求证：直线AF∥平面BEC₁
（2）求A到平面BEC₁的距离．

Answer 1

分析：（1）取BC₁的中点H，连接HE、HF，利用三角形中位线定理和棱柱的性质证出四边形AFHE为平行四边形，从而得到AF∥HE，结合线面平行判定定理即可证出直线AF∥平面BEC₁；
（2）由V_A-BEC1=V_C1-BEC利用等体积法建立关系式，根据正三棱柱ABC-A₁B₁C₁的性质，结合题中数据算出△BEC₁和△ABE的面积，以及C₁到平面AA₁B₁B的距离，代入前面的等式即可解出A到平面BEC₁的距离．

解答：解：（1）取BC₁的中点H，连接HE、HF，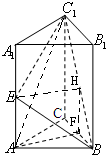
则△BCC₁中，HF∥CC₁且HF=

1

2

CC₁
又∵平行四边形AA₁C₁C中，AE∥CC₁且AE=

1

2

CC₁
∴AE∥HF且AE=HF，可得四边形AFHE为平行四边形，
∴AF∥HE，
∵AF?平面REC₁，HE?平面REC₁
∴AF∥平面REC₁．…（6分）
（2）等边△ABC中，高AF=

3

2

AB=

3

，所以EH=AF=

3

由三棱柱ABC-A₁B₁C₁是正三棱柱，得C₁到平面AA₁B₁B的距离等于

3

∵Rt△A₁C₁E≌Rt△ABE，∴EC₁=EB，得EH⊥BC₁
可得S_△ BEC1=

1

2

BC₁•EH=

1

2

×

42+22

×

3

=

15

，
而S_△ABE=

1

2

AB×BE=2
由等体积法得V_A-BEC1=V_C1-BEC，
∴

1

3

S_△ BEC1×d=

1

3

S_△ABE×

3

，（d为点A到平面BEC₁的距离）
即

1

3

×

15

×d=

1

3

×2×

3

，解之得d=

2 5

5

∴点A到平面BEC₁的距离等于

2 5

5

．…（12分）

点评：本题在正三棱柱中求证线面平行，并求点到平面的距离．着重考查了正三棱柱的性质、线面平行判定定理和等体积法求点到平面的距离等知识，属于中档题．