题目内容
5.己知数列{an}满足a1=1,$\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}}$=3,则数列{an}的通项公式为an=(3n-2)2.分析 通过数列{$\sqrt{{a}_{n}}$}是首项为1、公差为3的等差数列,进而计算可得结论.
解答 解:∵a1=1,$\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}}$=3,
∴数列{$\sqrt{{a}_{n}}$}是首项为1、公差为3的等差数列,
∴$\sqrt{{a}_{n}}$=1+3(n-1)=3n-2,
∴an=(3n-2)2,
故答案为:(3n-2)2.
点评 本题考查数列的通项,注意解题方法的积累,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.过点C(-1,1)和D(1,3),圆心在x轴上的圆的方程是( )
| A. | x2+(y-2)2=10 | B. | x2+(y+2)2=10 | C. | (x-2)2+y2=10 | D. | (x+2)2+y2=10 |
17.如图各网格是单位正方形,粗线所表示的图形为某几何体的三视图.则该几何体的体积为( )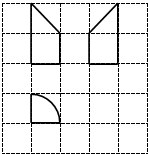

| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
15.函数y=cos(ωx+$\frac{π}{2}$)在[0,$\frac{π}{4}$]上为增函数,则ω的取值范围为( )
| A. | [-2,0) | B. | [-3,0) | C. | [-2,2] | D. | (0,2] |
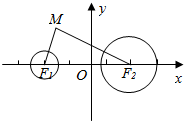 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.


