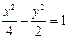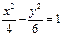题目内容

设双曲线的中心在坐标原点，对称轴是坐标轴，F1、F2是左、右焦点，是双曲线上一点，且∠F1PF2=600，S△PF1F2=12
3
，又离心率为2，求双曲线的方程．
不妨设点P在双曲线的右支上，
设双曲线的方程为
x2
a2
-
y2
b2
=1，|PF1|=m，|PF2|=n则有
m-n=2a①
∠F1PF2=600
由余弦定理得
m2+n2-2mncos60°=4c2②
∵S△PF1F2=12
3

∴
1
2
mnsin60°=12
3
③
∵离心率为2
∴
c
a
=2④
解①②③④a=2，c=4
∴b2=c2-a2=12
双曲线的方程为
x2
4
-
y2
12
=1．
练习册系列答案
相关题目
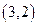求过点且与椭圆有相同焦点的双曲线的方程。
椭圆的中心在原点，焦距为4，一条准线为x=3，则该椭圆的方程为（　　）
A．
x2
6
+
y2
2
=1		B．
x2
4
+
y2
2
=1		C．
y2
4
+
x2
2
=1		D．
y2
6
+
x2
2
=1
求下列双曲线的标准方程：
（1）过点（3，-1），渐近线方程是y=±3x；
（2）与椭圆
x2
16
+
y2
64
=1有相同的焦点，且离心率为
2
．
已知双曲线经过点P（-3，2
7
）和点Q（-6
2
，7），求此双曲线的标准方程．
双曲线
x2
9
-
y2
4
=1左支上一点P到其左、右两焦点F1、F2的距离之和为8，则点P到左焦点F1的距离是（　　）
A．9B．7C．4D．1
分别求适合下列条件圆锥曲线的标准方程：
（1）焦点为F1（0，-1）、F2（0，1）且过点M(
3
2
，1)椭圆；
（2）与双曲线x2-
y2
2
=1有相同的渐近线，且过点（2，2）的双曲线．
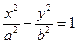若双曲线的两个焦点到一条准线的距离之比为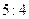，则双曲线的离心率为（  ）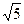
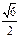A．3B．9C．D．5
下列曲线中离心率为的是(     )
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网