题目内容
(本小题满分9分)
已知函数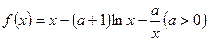 。
。
(Ⅰ)当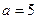 时,求函数
时,求函数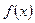 的单调递增区间;
的单调递增区间;
(Ⅱ)求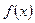 的极大值;
的极大值;
(Ⅲ)求证:对于任意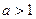 ,函数
,函数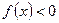 在
在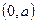 上恒成立。
上恒成立。
解:定义域为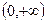 ,且
,且
(Ⅰ)当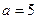 时,
时, ,令
,令 ,
,
解得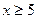 或
或 。故函数
。故函数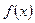 在
在 ,
, 上单调递增。 …………2分
上单调递增。 …………2分
(Ⅱ)令 ,即
,即 ,
,
当 时,上式化为
时,上式化为 恒成立。故
恒成立。故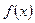 在
在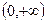 上单调递增,无极值;
上单调递增,无极值;
当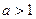 时,解得
时,解得 或
或 。故
。故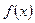 在
在 ,
,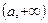 上单调递增,在
上单调递增,在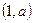 上单调递减。
上单调递减。

1 

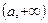

+ 0 - 0 + 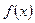
增 极大值 减 极小值 增
故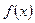 在
在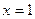 处有极大值
处有极大值 。
。
当 时,解得
时,解得 或
或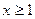 。故
。故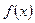 在
在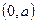 ,
, 解析
解析

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点. ,
,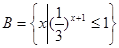 ,求(
,求( RA)
RA)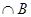
 ,
, 是同一平面内的两个向量,其中
是同一平面内的两个向量,其中 ,
, 且
且 与
与 垂直,(1)求
垂直,(1)求 ;
; 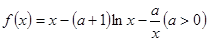 。
。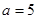 时,求函数
时,求函数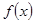 的单调递增区间;
的单调递增区间; ,函数
,函数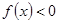 在
在 上恒成立。
上恒成立。