题目内容
在矩形ABCD中，AB=4，BC=3，沿AC将矩形ABCD折叠，其正视图和俯视图如图所示．此时连接顶点B、D形成三棱锥B-ACD，则其侧视图的面积为（ ）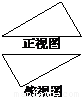
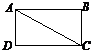
A．
B．
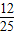
C．
D．
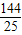
【答案】分析：由题意可知所折叠的平面ABC与平面ACD垂直，三棱锥B-ACD侧视图为等腰直角三角形，AD是斜边，两条直角边分别是过B和D向AC所做的垂线，做出直角边的长度，得到侧视图的面积．
解答：解：由正视图和俯视图可知平面ABC⊥平面ACD．
三棱锥B-ACD侧视图为等腰直角三角形，AD是斜边，
两条直角边分别是过B和D向AC所做的垂线，
直角边长为
，
∴侧视图面积为
．
故选C．
点评：本题考查简单几何体的三视图，根据所给的两个三视图得到直观图，这是三视图经常考查的知识点，是一个基础题．
解答：解：由正视图和俯视图可知平面ABC⊥平面ACD．
三棱锥B-ACD侧视图为等腰直角三角形，AD是斜边，
两条直角边分别是过B和D向AC所做的垂线，
直角边长为
，∴侧视图面积为
．故选C．
点评：本题考查简单几何体的三视图，根据所给的两个三视图得到直观图，这是三视图经常考查的知识点，是一个基础题．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=3
如图，在矩形ABCD中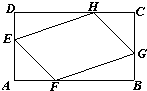，已知AD=2，AB=a（a＞2），E、F、G、H分别是边AD、AB、BC、CD上的点，若AE=AF=CG=CH，问AE取何值时，四边形EFGH的面积最大？并求最大的面积．
的取值范围．
|=
.设
=a, 
=b, 
=c,求|a+b+c|.